这两天钻我的模拟赛钻得思想僵化了,本来打算弃考,最后半小时才决定手糊一波。
T1
原题……$dp$ / $bfs$ 都行(因为所有边权都是 $1$,第一次扩展到的就是最短路)。
然而我判错了向左走的情况,一下被爆了,降智。

1 #include<bits/stdc++.h> 2 using namespace std; 3 inline int read(){ 4 int x=0; bool f=1; char c=getchar(); 5 for(;!isdigit(c);c=getchar()) if(c=='-') f=0; 6 for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^'0'); 7 if(f) return x; 8 return 0-x; 9 } 10 int a,b,dp[200002]; 11 int main(){ 12 freopen("meet.in","r",stdin); 13 freopen("meet.out","w",stdout); 14 a=read(),b=read(); 15 memset(dp,0x7f,sizeof dp); 16 dp[a]=0; 17 for(int i=a-1;i>=0;--i) dp[i]=dp[i+1]+1; 18 for(int i=0;i<=b;++i){ 19 dp[i+1]=min(dp[i+1],dp[i]+1); 20 if((i<<1)-1<=b) dp[i<<1]=min(dp[i<<1],dp[i]+1), dp[(i<<1)-1]=min(dp[(i<<1)-1],dp[i]+2); 21 } 22 printf("%d ",dp[b]); 23 return 0; 24 }
T2
我之前做过类似的题,然后现在又忘了-_- 再次降智
题解 $pdf$ 里面貌似写的很清楚了……
必定先考虑全是 $1$ 的情况。打个暴力,然后仔细观察矩阵中每个数是怎么转移来的,发现就是它上面和左面的数相加得到。
那这不就是个斜的杨辉三角么?
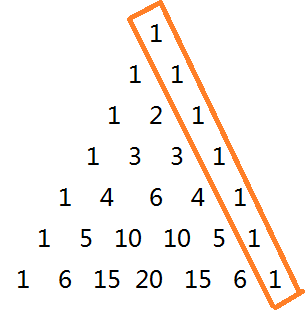
如图,最右边一行(橙框部分)是初始序列,然后每操作一次,序列就变为左下一行。
这是初始序列全是 $1$ 的情况,那对于任意初始序列的情况呢?
我们发现,最终序列的每个数,是由初始序列中每个数 乘上很多次得来的。
那系数是多少?
假设杨辉三角从第 $0$ 行第 $0$ 列算起(方便求组合数),则操作 $k$ 次后,第 $i$ 个数 $=$ $C_{k+i-2}^{i-1} imes a_1+C_{k+i-3}^{i-2} imes a_2+C_{k+i-4}^{i-3} imes a_3+...+C_{k-1}^{0} imes a_i$,其中 $a$ 为初始序列。具体举例可以看 $pdf$。
系数反过来对应的原因是杨辉三角每个数的累加量是前缀和,而本题序列每个数的累加量是后缀和(前面的数离后面的数多远,前面的数就被算多少次)。
由于杨辉三角的对称性,反过来推序列也是一样的,每个数的计算公式 改一下上面那个就得到了。

由上述公式可知,第 $k$ 行的每个数被后面的数累加时的系数 只有 $n$ 种,又因为组合数 $C$ 的上面一项最多只有 $n$,所以可以预处理 $n$ 以内的逆元,再 $O(n^2)$ 暴力求出 $n$ 种系数(每个组合数最多是乘 $n$ 个数再除以 $n$ 个数,暴力计算的复杂度是 $O(n)$),最后用上述公式,把每个数前面的数都乘以对应的系数,累加即可求出这个数。时间复杂度 $O(n^2)$。

1 #include<bits/stdc++.h> 2 #define int long long 3 using namespace std; 4 inline int read() 5 { 6 int x = 0,f = 1;char ch = getchar(); 7 for(;!isdigit(ch);ch = getchar())if(ch == '-')f = -f; 8 for(;isdigit(ch);ch = getchar())x = 10 * x + ch - '0'; 9 return x * f; 10 } 11 const int maxn = 5010,mod = 1e9 + 7; 12 int n,k;int a[maxn],s[maxn],Inv[maxn]; 13 inline int ksm(int x,int t) 14 { 15 int res = 1; 16 while(t) 17 { 18 if(t & 1)res = res * x % mod; 19 x = x * x % mod; 20 t = t >> 1; 21 } 22 return res; 23 } 24 inline int inv(int x){return ksm(x,mod - 2);} 25 /*sig (1~x) from (x + k - i) choose (i) * a[0][i]*/ 26 inline int C(int n,int m) 27 { 28 if(n < m || n < 0 || m < 0)return 0; 29 int cur = n,ans = 1; 30 for(int i=m;i>=1;i--) 31 { 32 (ans *= cur) %= mod; 33 (ans *= Inv[i]) %= mod; 34 cur--; 35 } 36 return ans; 37 } 38 int xs[maxn]; 39 signed main() 40 { 41 freopen("sum.in","r",stdin); 42 freopen("sum.out","w",stdout); 43 n = read();k = read() - 1; 44 //for(int i=1;i<=n+k;i++)fac[i] = fac[i - 1] * i % mod; 45 Inv[0] = 1; 46 for(int i=1;i<=n;i++)Inv[i] = inv(i); 47 for(int i=1;i<=n;i++)a[i] = read(); 48 //for(int i=1;i<=n;i++)a[i] -= a[i - 1]; 49 //for(int i=1;i<=n;i++)cout<<a[i]<<" "; 50 for(int i=1;i<=n;i++)xs[i] = C(i + k - 1,(i + k - 1) - k) % mod; 51 for(int i=1;i<=n;i++) 52 for(int j=1;j<=i;j++) 53 (s[i] += xs[i - j + 1] * a[j]) %= mod; 54 for(int i=1;i<=n;i++)printf("%lld ",s[i]); 55 }
T3
没好好想,瞎搞了一个时间复杂度不对的线段树就交上去了。

1 #include<bits/stdc++.h> 2 #define ll long long 3 #define N 100002 4 #define M 200002 5 #define inf 1000000000 6 using namespace std; 7 inline int read(){ 8 int x=0; bool f=1; char c=getchar(); 9 for(;!isdigit(c);c=getchar()) if(c=='-') f=0; 10 for(; isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^'0'); 11 if(f) return x; 12 return 0-x; 13 } 14 int n,m,k; 15 ll ans; 16 struct input{ 17 int r,s,t; 18 inline bool operator <(const input x)const{ 19 return r>x.r; 20 } 21 }in[N]; 22 int L,R; 23 namespace SegmentTree{ 24 struct Tree{ 25 int tag,mx,mn; 26 }tr[M<<3]; 27 ll num[M]; 28 inline void pushdown(int o){ 29 if(tr[o].tag) 30 tr[o<<1].mx+=tr[o].tag, tr[o<<1].mn+=tr[o].tag, 31 tr[o<<1|1].mx+=tr[o].tag, tr[o<<1|1].mn+=tr[o].tag, 32 tr[o<<1].tag+=tr[o].tag, tr[o<<1|1].tag+=tr[o].tag, tr[o].tag=0; 33 } 34 inline void pushup(int o){tr[o].mx=max(tr[o<<1].mx,tr[o<<1|1].mx), tr[o].mn=min(tr[o<<1].mn,tr[o<<1|1].mn);} 35 void update(int o,int l,int r){ 36 //printf("udpate %d %d %d %d ",L,l,r,R); 37 if(L<=l && r<=R){ 38 ++tr[o].tag, ++tr[o].mx, ++tr[o].mn; 39 return; 40 } 41 pushdown(o); 42 int mid=(l+r)>>1; 43 if(L<=mid) update(o<<1,l,mid); 44 if(R>mid) update(o<<1|1,mid+1,r); 45 pushup(o); 46 } 47 ll query(int o,int l,int r){ 48 if(tr[o].mx==tr[o].mn){ 49 //printf("success %d %d ",l,r); 50 tr[o].mx=tr[o].mn=-inf, tr[o].tag=0; 51 return r-l+1; 52 } 53 //printf("tag:%d ",tr[o].tag); 54 pushdown(o); 55 //printf("revo %d %d %d %d %d %d ",l,r,tr[o].mx,tr[o<<1].mx,tr[o<<1|1].mx,tr[o].mn); 56 int mid=(l+r)>>1; ll ret=0; 57 if(tr[o<<1].mx==tr[o].mx) ret+=query(o<<1,l,mid); 58 if(tr[o<<1|1].mx==tr[o].mx) ret+=query(o<<1|1,mid+1,r); 59 pushup(o); 60 return ret; 61 } 62 }; 63 using namespace SegmentTree; 64 inline void action(int i,int l,int r){ 65 //printf("action:%d %d %d ",i,l,r); 66 L=l,R=r; 67 update(1,1,m); 68 if(tr[1].mx==k) ans+=query(1,1,m)*in[i].r*in[i].r; 69 // printf("%lld ",ans); 70 } 71 int main(){ 72 freopen("xiaoqiao.in","r",stdin); 73 freopen("xiaoqiao.out","w",stdout); 74 n=read(),m=read(),k=read(); 75 int i; 76 for(i=1;i<=n;++i) in[i].r=read(), in[i].s=read()+m+1, in[i].t=read()+m; 77 sort(in+1,in+n+1); 78 m<<=1; 79 for(i=1;i<=n;++i){ 80 if(in[i].s>in[i].t) action(i,in[i].s,m), action(i,1,in[i].t); 81 else action(i,in[i].s,in[i].t); 82 } 83 printf("%lld ",ans); 84 return 0; 85 }
容易发现 $query$ 的复杂度错了,不是 $log$ 级别的,然后就就被爆踩。
由于只需要求最终的全局情况,也就是说答案跟操作顺序没关系,我们可以搞离线。
于是想到扫描线。
扫描线是个啥东西?如图
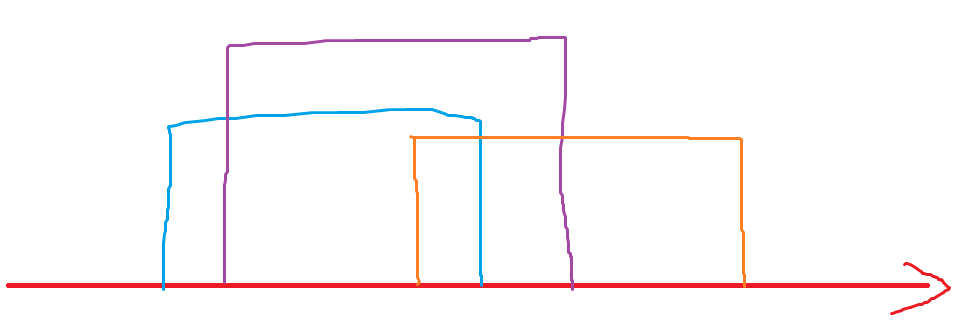
可以把问题同义转化一下:在墙上贴 $n$ 张底线相同、高度不同的海报,问有多大面积的区域至少被 $k$ 张海报覆盖。
然后我们在左端点搞一条扫描线(黑线)。
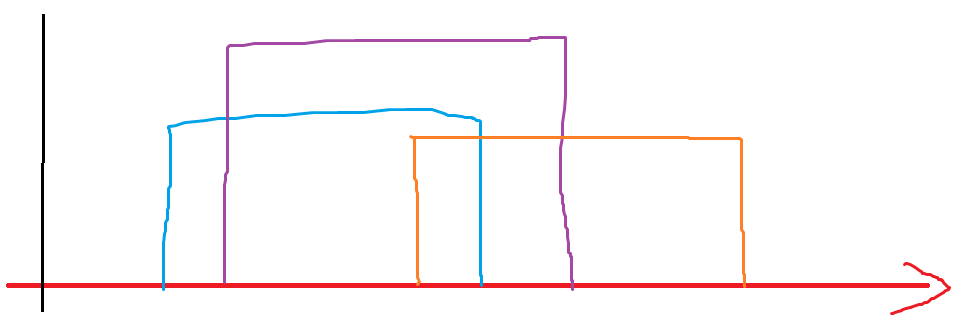
把扫描线不停往右移动,扫到下一个海报的左端点时,更新一下当前纵轴上的覆盖海报数(不能只 $+1$,因为可能有多个海报的左端点重合)。如果海报数 $ge k$,就二分出从下往上数第 $k$ 个海报端点的位置,它下面就是覆盖海报数 $ge k$ 的区域。
当扫描线扫到下一个位置时,累加它到上一个扫到的位置围出的 覆盖海报数 $ge k$ 的区域面积,并再做上述更新即可。
所以我们把每张海报拆成左右两个端点,现在问题就变成了维护一个数据结构,支持单点插入、单点删除、查询第 $k$ 大值。
复杂度基本是对的,因为最多有 $2m$ 张海报,也就是 $4m=400000$ 个端点,那总共就有 $400000$ 次插入、删除操作(两个加起来)。
查询第 $k$ 大值就看卡常优不优秀了。这是个比较板子的维护,一种方法是树状数组二分(弱智写法的总时间复杂度是 $O(n*log(n^2))$,优秀写法的总时间复杂度是 $O(n*log(n))$),一种方法是平衡树(韩神现场yy了一个没写过的 $SBT$ 就 $A$ 了;总时间复杂度 $O(n*log(n))$ 带常数),还有一种方法是权值线段树(树上自带二分,总时间复杂度 $O(n*log(high))$)。
由于树状数组的常数小,所以跑的甚至比平衡树快一点……

1 #include<bits/stdc++.h> 2 #define LL long long 3 using namespace std; 4 inline int read() 5 { 6 int x = 0,f = 1;char ch = getchar(); 7 for(;!isdigit(ch);ch = getchar())if(ch == '-')f = -f; 8 for(;isdigit(ch);ch = getchar())x = 10 * x + ch - '0'; 9 return x * f; 10 } 11 const int maxn = 400005; 12 int n,m,kk; 13 int top1,top2; 14 struct qwq{int l,r,R;}nega[maxn],posi[maxn]; 15 struct ques{int st,r;char f;bool operator < (const ques &b)const{return st<b.st;}}opts[maxn]; 16 17 namespace RP 18 { 19 struct node{int ls,rs,size,val;}tr[maxn << 2]; 20 int dfn,root,ops; 21 inline void pushup(int x){tr[x].size=tr[tr[x].ls].size+tr[tr[x].rs].size+1;} 22 inline void lt(int &x) 23 { 24 int k=tr[x].rs;tr[x].rs=tr[k].ls; 25 tr[k].ls=x;tr[k].size=tr[x].size; 26 pushup(x); 27 x=k; 28 } 29 inline void rt(int &x) 30 { 31 int k=tr[x].ls;tr[x].ls=tr[k].rs; 32 tr[k].rs=x;tr[k].size=tr[x].size; 33 pushup(x); 34 x=k; 35 } 36 inline int rng() 37 { 38 static unsigned long long seed = 233333333333333333LL; 39 seed = seed + (seed << 17) + 531433123515; 40 return seed; 41 } 42 /* 43 void rp() 44 { 45 int x; 46 for(int i=1;i<=min(n,10);i++)lt(x = rng() % n + 1); 47 for(int i=1;i<=min(n,10);i++)rt(x = rng() % n + 1); 48 } 49 */ 50 inline void magic(int &x,char f) 51 { 52 if(f) 53 { 54 if(tr[tr[tr[x].ls].ls].size > tr[tr[x].rs].size) rt(x),rt(x); 55 else if(tr[tr[tr[x].ls].rs].size > tr[tr[x].rs].size) lt(tr[x].ls),rt(x); 56 else return; 57 } 58 else 59 { 60 if (tr[tr[tr[x].rs].rs].size > tr[tr[x].ls].size) lt(x); 61 else if (tr[tr[tr[x].rs].ls].size > tr[tr[x].ls].size) rt(tr[x].rs),lt(x); 62 else return; 63 } 64 if(rng() & 1)lt(x); //Lucky! 65 magic(tr[x].ls,0);magic(tr[x].rs,1); 66 return; 67 } 68 inline void Insert(int &x,int v) 69 { 70 if (!x) 71 { 72 x = ++dfn; 73 tr[x].ls = tr[x].rs = 0; 74 tr[x].size = 1; 75 tr[x].val = v; 76 //rp(); 77 } 78 else 79 { 80 tr[x].size++; 81 if (v<tr[x].val) Insert(tr[x].ls,v); 82 else Insert(tr[x].rs,v); 83 magic(x,v < tr[x].val); 84 } 85 } 86 inline int del(int &x,int v) 87 { 88 tr[x].size--; 89 int k = tr[x].val; 90 if (v == k || (v < k && !tr[x].ls) || (v > k && !tr[x].rs) ) 91 { 92 if (!tr[x].ls || !tr[x].rs) x = tr[x].ls + tr[x].rs; 93 else tr[x].val = del(tr[x].ls,v + 1); 94 return k; 95 } 96 else 97 { 98 if (v < k) return del(tr[x].ls,v); 99 else return del(tr[x].rs,v); 100 } 101 } 102 inline int kth(int k) 103 { 104 int x = root; 105 while(tr[tr[x].ls].size + 1 != k) 106 { 107 if(tr[tr[x].ls].size+1 < k) k -= tr[tr[x].ls].size,k--,x = tr[x].rs; 108 else x = tr[x].ls; 109 } 110 return tr[x].val; 111 } 112 } 113 using namespace RP; 114 int main() 115 { 116 freopen("xiaoqiao.in","r",stdin); 117 freopen("xiaoqiao.out","w",stdout); 118 n = read(),m = read(),kk = read(); 119 for(int i=1;i<=n;i++) 120 { 121 int R = read(),l = read(),r = read(); 122 if(l == m) l = -m; 123 if(r == -m) r = m; 124 if(l == r) continue; 125 if(l >= 0 && r >= 0) 126 { 127 if(l > r) 128 { 129 if(m) nega[++top1]=(qwq){-m,0,R}; 130 if(l != m) posi[++top2]=(qwq){l,m,R}; 131 132 if(r) posi[++top2]=(qwq){0,r,R}; 133 } 134 else posi[++top2]=(qwq){l,r,R}; 135 } 136 else if(l <= 0 && r <= 0) 137 { 138 if(l > r) 139 { 140 if(l) nega[++top1]=(qwq){l,0,R}; 141 if(r != -m) nega[++top1]=(qwq){-m,r,R}; 142 143 if(m) posi[++top2]=(qwq){0,m,R}; 144 } 145 else nega[++top1]=(qwq){l,r,R}; 146 } 147 else if (l <= 0 && r >= 0) 148 { 149 if (l) nega[++top1]=(qwq){l,0,R}; 150 if (r) posi[++top2]=(qwq){0,r,R}; 151 } 152 else if(l >= 0 && r <= 0) 153 { 154 nega[++top1]=(qwq){-m,r,R}; 155 posi[++top2]=(qwq){l,m,R}; 156 } 157 } 158 LL res1 = 0,res2 = 0; 159 160 root = dfn = ops = 0; 161 for(int i=1;i<=top1;i++) 162 { 163 opts[++ops] = (ques){nega[i].l,nega[i].R,1}; 164 opts[++ops] = (ques){nega[i].r,nega[i].R,0}; 165 } 166 sort(opts + 1,opts + ops + 1); 167 int last = opts[1].st; 168 int l = 1,r = 1; 169 while(l <= ops) 170 { 171 while(r <= ops && opts[r].st == opts[l].st) r++; 172 if(tr[root].size >= kk) 173 { 174 LL x = kth(tr[root].size - kk + 1); //di k da = n - k + 1 xiao 175 res1 += x * x * (opts[l].st - last); 176 } 177 for(int i=l;i<r;i++) 178 { 179 if(opts[i].f == 1) Insert(root,opts[i].r); 180 else del(root,opts[i].r); 181 } 182 last = opts[l].st; 183 l = r; 184 } 185 186 root = dfn = ops = 0; 187 for(int i=1;i<=top2;i++) 188 { 189 opts[++ops] = (ques){posi[i].l,posi[i].R,1}; 190 opts[++ops] = (ques){posi[i].r,posi[i].R,0}; 191 } 192 sort(opts + 1,opts + ops + 1); 193 last = opts[1].st; 194 l = 1,r = 1; 195 while(l <= ops) 196 { 197 while(r <= ops && opts[r].st == opts[l].st) r++; 198 if(tr[root].size >= kk) 199 { 200 LL x = kth(tr[root].size - kk + 1); //di k da = n - k + 1 xiao 201 res2 += x * x * (opts[l].st - last); 202 } 203 for(int i=l;i<r;i++) 204 { 205 if(opts[i].f == 1) Insert(root,opts[i].r); 206 else del(root,opts[i].r); 207 } 208 last = opts[l].st; 209 l = r; 210 } 211 cout<<res1 + res2; 212 }

1 #include<bits/stdc++.h> 2 #define rep(i,x,y) for(int i=(x);i<=(y);++i) 3 #define dwn(i,x,y) for(int i=(x);i>=(y);--i) 4 #define LL long long 5 #define maxn 200010 6 using namespace std; 7 int read() 8 { 9 int x=0,f=1;char ch=getchar(); 10 while(!isdigit(ch)&&ch!='-')ch=getchar(); 11 if(ch=='-')ch=getchar(),f=-1; 12 while(isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar(); 13 return x*f; 14 } 15 void write(LL x) 16 { 17 if(x==0){putchar('0'),putchar(' ');return;} 18 if(x<0)putchar('-'),x=-x; 19 int f=0;char ch[20]; 20 while(x)ch[++f]=x%10+'0',x/=10; 21 while(f)putchar(ch[f--]); 22 putchar(' '); 23 return; 24 } 25 int n,m,k,qr,qs,qt,tr[maxn]; 26 int tpr; 27 LL ans; 28 int lt(int x){return x&(-x);} 29 void add(int x,int k){for(;x<=tpr;x+=lt(x))tr[x]+=k;return;} 30 int ask(int x){int k=0;for(;x;x-=lt(x))k+=tr[x];return k;} 31 vector<int>ad[maxn],de[maxn]; 32 int gx(int x){return m-x;} 33 int nxt(int x){if(x>(m<<1))return x-(m<<1);if(x<1)return (m<<1)-x;return x;} 34 int main() 35 { 36 freopen("xiaoqiao.in","r",stdin); 37 freopen("xiaoqiao.out","w",stdout); 38 n=read(),m=read(),k=read(); 39 rep(i,1,n) 40 { 41 qr=read(),qs=read(),qt=read(); 42 qs=gx(qs),qt=gx(qt),qt=nxt(qt+1),qs=nxt(qs),swap(qs,qt); 43 if(qs<=qt) 44 { 45 ad[qs].push_back(qr),de[qt+1].push_back(qr); 46 } 47 else 48 { 49 ad[1].push_back(qr),de[qt+1].push_back(qr); 50 ad[qs].push_back(qr),de[m*2+1].push_back(qr); 51 } 52 tpr=max(tpr,qr); 53 }tpr++;int li=m*2; 54 rep(i,1,li) 55 { 56 int lim=ad[i].size()-1; 57 rep(j,0,lim)add(1,1),add(ad[i][j]+1,-1); 58 lim=de[i].size()-1; 59 rep(j,0,lim)add(1,-1),add(de[i][j]+1,1); 60 int L=1,R=tpr,maxl=0; 61 while(L<=R) 62 { 63 int mid=(L+R>>1); 64 int tmp=ask(mid); 65 if(tmp>=k)maxl=max(maxl,mid),L=mid+1; 66 else R=mid-1; 67 } 68 ans+=(LL)maxl*(LL)maxl; 69 } 70 write(ans); 71 return 0; 72 }
