本来实在写不动这题 sol 了,但一想这是个经典的模型转化问题,于是就写了(.jpg)
题意
有一个序列 (a_i)。
两人轮流操作,每次操作为二选一:
1. 把最大的 (a_i) 减成 (0)
2. 把所有非 (0) 的 (a_i) 减去 (1)
若一个人操作后,所有 (a_i) 都是 (0),这个人就输了。
两人都采用轮流策略,问谁能赢。
(nle 10^5)
(a_ile 10^9)
题解
智商模型转化:把所有 (a_i) 从大到小排序,画一个柱状图,第 (i) 个柱子的高度为 (a_i)。每个人可以删去最左边一列或最下边一行,求谁操作后删光整个柱状图。
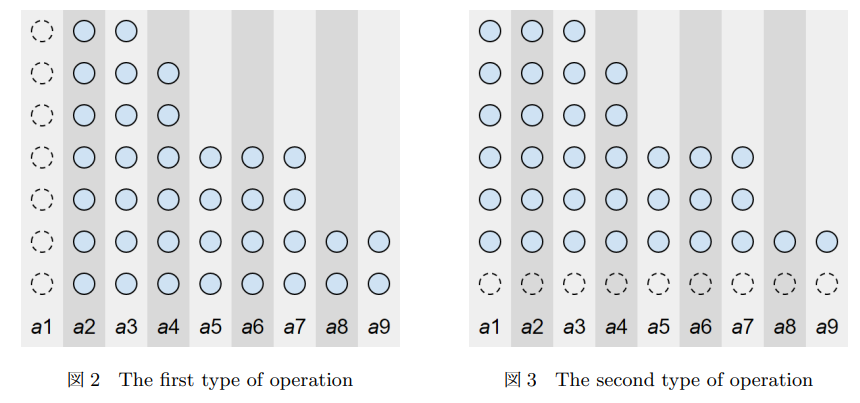
我们发现每次操作后,图的左下角一定会移动,并且一个左下角对应一种游戏局面。
所以,这个模型还可以转化:从左下角出发,两人轮流向上或向右走一个单位,走到边界的人输。
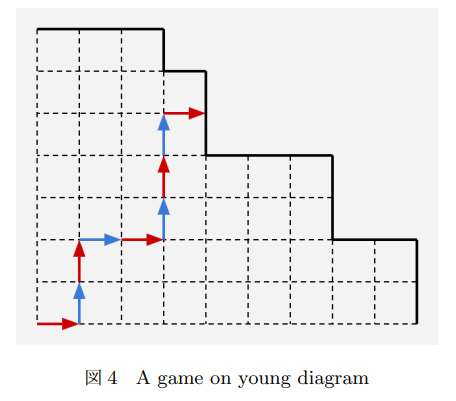
这是个很简单的博弈论 ( ext{dp}),每个点对应一个操作者的必胜态 / 必败态。将操作者的胜败状态记在该操作到达的点上,则边界上全是必败态,((1,1)) 是后手的胜败状态(因为先手从这里出发到邻点,胜败状态在两个邻点上,通过那两个点的胜败状态算出的胜败状态 相当于后手在游戏开始时的胜败状态)。
直接 (O(n imes a_i)) ( ext{dp}) 即可求出每个点是必胜态还是必败态。
但这样显然会 T,我们考虑优化。
随便画一个图,手玩出每个点的胜败状态(红圈表示必败态,蓝叉表示必胜态)
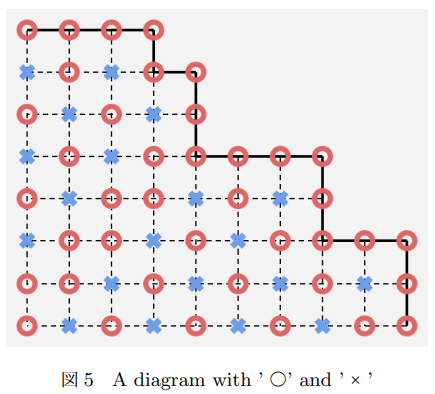
不难发现左下-右上对角线上的状态都是一样的!如何证明?
假如 ((x,y)) 是 (1),((x-1,y-1)) 不可能是 (0)。这里用反证法,举一个例子:
0 ?
1 1 ?
0 1 0
注意到 (0) 的后继全都是 (1),(1) 的后继一定有 (0)。
可以画出这样的图。
发现两个 ? 处至少有一个 (0)((1) 的后继一定有 (0)),但两个 ? 处都必须是 (1)((0) 的后继全部是 (1)),因此矛盾。
以上图为例,我们就只需要算 ((4,4)) 的胜败状态了!
这个位置怎么算呢?
它的上边、右边所有点都贴着边界,状态为胜、败轮流交替。于是可以从
以上图为例,从 ((4,7)) 往下根据奇偶性推出 ((4,5)) 的状态,从 ((8,4)) 往左推出 ((5,4)) 的状态,然后根据 ((4,5)) 和 ((5,4)) 的状态就可以推出 ((4,4)longrightarrow (1,1)) 的状态了。
复杂度 (O(n))。
#include<bits/stdc++.h>
using namespace std;
int a[100005];
int main(){
int n,i;
scanf("%d",&n);
for(i=1; i<=n; ++i) scanf("%d",&a[i]);
sort(a+1, a+n+1, greater<int>());
for(i=1; i<=n; ++i){
if(i<=a[i] && a[i+1]<i+1){
int j=0;
while(a[j+i+1]==i) j++;
if((a[i]-i)%2==0 && j%2==0) puts("Second");
else puts("First");
return 0;
}
}
}