Problem Description
Tour operator Your Personal Holiday organises guided bus trips across the Benelux. Every day the bus moves from one city S to another city F. On this way, the tourists in the bus can see the sights alongside the route travelled. Moreover, the bus makes a number of stops (zero or more) at some beautiful cities, where the tourists get out to see the local sights.
Different groups of tourists may have different preferences for the sights they want to see, and thus for the route to be taken from S to F. Therefore, Your Personal Holiday wants to offer its clients a choice from many different routes. As hotels have been booked in advance, the starting city S and the final city F, though, are fixed. Two routes from S to F are considered different if there is at least one road from a city A to a city B which is part of one route, but not of the other route.
There is a restriction on the routes that the tourists may choose from. To leave enough time for the sightseeing at the stops (and to avoid using too much fuel), the bus has to take a short route from S to F. It has to be either a route with minimal distance, or a route which is one distance unit longer than the minimal distance. Indeed, by allowing routes that are one distance unit longer, the tourists may have more choice than by restricting them to exactly the minimal routes. This enhances the impression of a personal holiday.
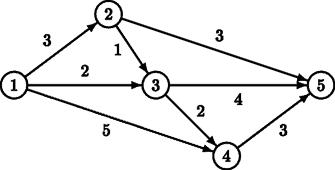
For example, for the above road map, there are two minimal routes from S = 1 to F = 5: 1 → 2 → 5 and 1 → 3 → 5, both of length 6. There is one route that is one distance unit longer: 1 → 3 → 4 → 5, of length 7.
Now, given a (partial) road map of the Benelux and two cities S and F, tour operator Your Personal Holiday likes to know how many different routes it can offer to its clients, under the above restriction on the route length.
Different groups of tourists may have different preferences for the sights they want to see, and thus for the route to be taken from S to F. Therefore, Your Personal Holiday wants to offer its clients a choice from many different routes. As hotels have been booked in advance, the starting city S and the final city F, though, are fixed. Two routes from S to F are considered different if there is at least one road from a city A to a city B which is part of one route, but not of the other route.
There is a restriction on the routes that the tourists may choose from. To leave enough time for the sightseeing at the stops (and to avoid using too much fuel), the bus has to take a short route from S to F. It has to be either a route with minimal distance, or a route which is one distance unit longer than the minimal distance. Indeed, by allowing routes that are one distance unit longer, the tourists may have more choice than by restricting them to exactly the minimal routes. This enhances the impression of a personal holiday.

For example, for the above road map, there are two minimal routes from S = 1 to F = 5: 1 → 2 → 5 and 1 → 3 → 5, both of length 6. There is one route that is one distance unit longer: 1 → 3 → 4 → 5, of length 7.
Now, given a (partial) road map of the Benelux and two cities S and F, tour operator Your Personal Holiday likes to know how many different routes it can offer to its clients, under the above restriction on the route length.
Input
The first line of the input file contains a single number: the number of test cases to follow. Each test case has the following format:
One line with two integers N and M, separated by a single space, with 2 ≤ N ≤ 1,000 and 1 ≤ M ≤ 10, 000: the number of cities and the number of roads in the road map.
M lines, each with three integers A, B and L, separated by single spaces, with 1 ≤ A, B ≤ N, A ≠ B and 1 ≤ L ≤ 1,000, describing a road from city A to city B with length L.
The roads are unidirectional. Hence, if there is a road from A to B, then there is not necessarily also a road from B to A. There may be different roads from a city A to a city B.
One line with two integers S and F, separated by a single space, with 1 ≤ S, F ≤ N and S ≠ F: the starting city and the final city of the route.
There will be at least one route from S to F.
One line with two integers N and M, separated by a single space, with 2 ≤ N ≤ 1,000 and 1 ≤ M ≤ 10, 000: the number of cities and the number of roads in the road map.
M lines, each with three integers A, B and L, separated by single spaces, with 1 ≤ A, B ≤ N, A ≠ B and 1 ≤ L ≤ 1,000, describing a road from city A to city B with length L.
The roads are unidirectional. Hence, if there is a road from A to B, then there is not necessarily also a road from B to A. There may be different roads from a city A to a city B.
One line with two integers S and F, separated by a single space, with 1 ≤ S, F ≤ N and S ≠ F: the starting city and the final city of the route.
There will be at least one route from S to F.
Output
For every test case in the input file, the output should contain a single number, on a single line: the number of routes of minimal length or one distance unit longer. Test cases are such, that this number is at most 10^9 = 1,000,000,000.
Sample Input
2
5 8
1 2 3
1 3 2
1 4 5
2 3 1
2 5 3
3 4 2
3 5 4
4 5 3
1 5
5 6
2 3 1
3 2 1
3 1 10
4 5 2
5 2 7
5 2 7
4 1
5 8
1 2 3
1 3 2
1 4 5
2 3 1
2 5 3
3 4 2
3 5 4
4 5 3
1 5
5 6
2 3 1
3 2 1
3 1 10
4 5 2
5 2 7
5 2 7
4 1
Sample Output
3
2
2
×××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××
×××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××××

1 /* 2 vis[i][1]表示第i个点在次短路径上已访问 3 vis{[i][0]表示第i个点在最短路径上已访问 4 count1[i][0]表示最短路径的条数 5 count1[i][1]表示次短路径的条数 6 dis[i][0]表示最短路径的长度 7 dis[i][1]表示次短路径的长度 8 用dijstra 9 if(此时路径<最短路径) 10 更新最短路 11 else if(此时路径==最短路径) 12 更新路径的数量 13 else if(此时路径<最短路径) 14 更新次短路径 15 else if(此时路径==次短路径) 16 更新路径的数量 17 */ 18 #include<iostream> 19 #include<string> 20 #include<cstring> 21 #include<cmath> 22 #include<cstdio> 23 #include<algorithm> 24 using namespace std; 25 const int inf=1<<30; 26 struct node 27 { 28 int cap; 29 int next; 30 int to; 31 }e[10011]; 32 int head[1001]; 33 int vis[1001][2],n,m; 34 int cas,src,endt,cnt; 35 int dis[1001][2],count1[1001][2]; 36 void add_edge(int a,int b,int cw) 37 { 38 e[cnt].to=b; 39 e[cnt].cap=cw; 40 e[cnt].next=head[a]; 41 head[a]=cnt++; 42 } 43 44 void dijstra() 45 { 46 memset(count1,0,sizeof(count1)); 47 memset(vis,0,sizeof(vis)); 48 int it,jt,tmp,k,flag; 49 for(it=1;it<=n;it++) 50 { 51 dis[it][0]=inf; 52 dis[it][1]=inf; 53 } 54 dis[src][0]=0; 55 count1[src][0]=1; 56 for(it=1;it<2*n;it++) 57 { 58 tmp=inf; 59 for(jt=1;jt<=n;jt++) 60 { 61 if(!vis[jt][0]&&tmp>dis[jt][0]) 62 { 63 flag=0; 64 k=jt; 65 tmp=dis[jt][0]; 66 } 67 else 68 if(!vis[jt][1]&&tmp>dis[jt][1]) 69 { 70 flag=1; 71 k=jt; 72 tmp=dis[jt][1]; 73 } 74 } 75 if(tmp==inf) 76 break; 77 vis[k][flag]=1; 78 for(jt=head[k];jt!=-1;jt=e[jt].next) 79 { 80 int v=e[jt].to; 81 if(dis[v][0]>tmp+e[jt].cap) 82 { 83 count1[v][1]=count1[v][0]; 84 dis[v][1]=dis[v][0]; 85 dis[v][0]=tmp+e[jt].cap; 86 count1[v][0]=count1[k][flag]; 87 } 88 else 89 if(dis[v][0]==tmp+e[jt].cap) 90 { 91 count1[v][0]+=count1[k][flag]; 92 } 93 else 94 if(dis[v][1]>tmp+e[jt].cap) 95 { 96 dis[v][1]=tmp+e[jt].cap; 97 count1[v][1]=count1[k][flag]; 98 } 99 else 100 if(dis[v][1]==tmp+e[jt].cap) 101 count1[v][1]+=count1[k][flag]; 102 } 103 } 104 } 105 int main() 106 { 107 int v,u,w; 108 scanf("%d",&cas); 109 while(cas--) 110 { 111 cnt=0; 112 memset(head,-1,sizeof(head)); 113 scanf("%d %d",&n,&m); 114 while(m--) 115 { 116 scanf("%d%d%d",&v,&u,&w); 117 add_edge(v,u,w); 118 119 } 120 scanf("%d %d",&src,&endt); 121 dijstra(); 122 int ans=count1[endt][0]; 123 if(dis[endt][1]==dis[endt][0]+1)//满足条件,再加 124 ans+=count1[endt][1]; 125 printf("%d ",ans); 126 } 127 return 0; 128 }
