Problem Description
1. It is a Strongly Connected graph.
2. Each edge of the graph belongs to a circle and only belongs to one circle.
We call this graph as CACTUS.
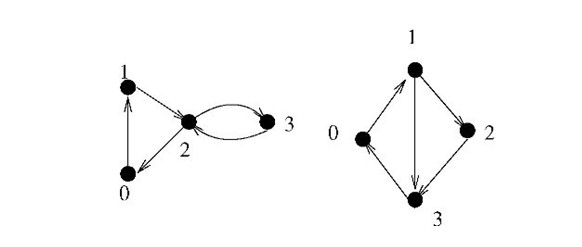
There is an example as the figure above. The left one is a cactus, but the right one isn’t. Because the edge (0, 1) in the right graph belongs to two circles as (0, 1, 3) and (0, 1, 2, 3).
2. Each edge of the graph belongs to a circle and only belongs to one circle.
We call this graph as CACTUS.

There is an example as the figure above. The left one is a cactus, but the right one isn’t. Because the edge (0, 1) in the right graph belongs to two circles as (0, 1, 3) and (0, 1, 2, 3).
Input
The input consists of several test cases. The first line contains an integer T (1<=T<=10), representing the number of test cases.
For each case, the first line contains a integer n (1<=n<=20000), representing the number of points.
The following lines, each line has two numbers a and b, representing a single-way edge (a->b). Each case ends with (0 0).
Notice: The total number of edges does not exceed 50000.
For each case, the first line contains a integer n (1<=n<=20000), representing the number of points.
The following lines, each line has two numbers a and b, representing a single-way edge (a->b). Each case ends with (0 0).
Notice: The total number of edges does not exceed 50000.
Output
For each case, output a line contains “YES” or “NO”, representing whether this graph is a cactus or not.
Sample Input
2
4
0 1
1 2
2 0
2 3
3 2
0 0
4
0 1
1 2
2 3
3 0
1 3
0 0
4
0 1
1 2
2 0
2 3
3 2
0 0
4
0 1
1 2
2 3
3 0
1 3
0 0
Sample Output
YES
NO
NO
***************************************************************************************************************************

1 #include<iostream> 2 #include<string> 3 #include<cstring> 4 #include<cmath> 5 #include<cstdio> 6 #include<queue> 7 #include<algorithm> 8 using namespace std; 9 struct node 10 { 11 int next,v; 12 }e[50050]; 13 int head[20401],sizer; 14 bool udfs[20040],ins[20040]; 15 int dfn[20040],low[20040]; 16 int stk[20040]; 17 int n,m,i,j,k,top,step; 18 void add_edge(int u,int v) 19 { 20 e[sizer].v=v; 21 e[sizer].next=head[u]; 22 head[u]=sizer++; 23 } 24 void init() 25 { 26 memset(head,-1,sizeof(head)); 27 memset(ins,false,sizeof(ins)); 28 memset(udfs,false,sizeof(udfs)); 29 memset(dfn,-1,sizeof(dfn)); 30 top=-1; sizer=step=0; 31 } 32 bool tarjan(int u) 33 { 34 stk[++top]=u; 35 ins[u]=true; 36 dfn[u]=low[u]=step++; 37 int cnt=0; 38 for(int it=head[u];it!=-1;it=e[it].next) 39 { 40 int now=e[it].v; 41 if(udfs[now])return false;//重复走一个点,返回; 42 if(dfn[now]==-1) 43 { 44 if(!tarjan(now))return false; 45 if(low[now]>dfn[u])return false; 46 if(low[now]<dfn[u])cnt++; 47 if(cnt==2)return false; 48 low[u]=min(low[u],low[now]); 49 } 50 else if(ins[now]) 51 { 52 low[u]=min(low[u],dfn[now]); 53 cnt++; 54 if(cnt==2)return false; 55 } 56 } 57 udfs[u]=true; 58 return true; 59 } 60 61 int main() 62 { 63 int cas,u,v; 64 scanf("%d",&cas); 65 while(cas--) 66 { 67 init(); 68 scanf("%d",&n); 69 while(true) 70 { 71 scanf("%d%d",&u,&v); 72 if(u==0&&v==0) break; 73 add_edge(u,v); 74 } 75 bool flag=tarjan(0); 76 if(flag) 77 { 78 for(i=0;i<n;i++) 79 if(dfn[i]==-1) 80 { 81 flag=false; 82 break; 83 } 84 } 85 if(flag) 86 printf("YES "); 87 else 88 printf("NO "); 89 } 90 return 0; 91 }
