CF739C Alyona and towers

题意：维护区间最大的先上升后下降的子段长度，支持区间加

这个题似乎很熟悉，想必你肯定做过它的简化版——最大上升子序列

那么遇到这样的题我们应该怎么做呢，别着急，我们一步一步来

• 我们肯定是要用线段树维护答案，那么左右儿子怎么合并答案呢，有这么几种情况：

• 前两种情况就是继承左右儿子的(ans)

• 第三种是左儿子中以右端点结尾的(ans+)右儿子中以左端点开始的最长下降序列长度（左儿子的右端点(>)右儿子的左端点）

• 第四种是右儿子中以左端点开始的(ans+)左儿子中以右端点结束的最长上升序列长度（左儿子的左端点(<)右儿子的左端点）

• 维护以左右端点开始或结尾的(zans,yans)也是类似的，以(zans)来说

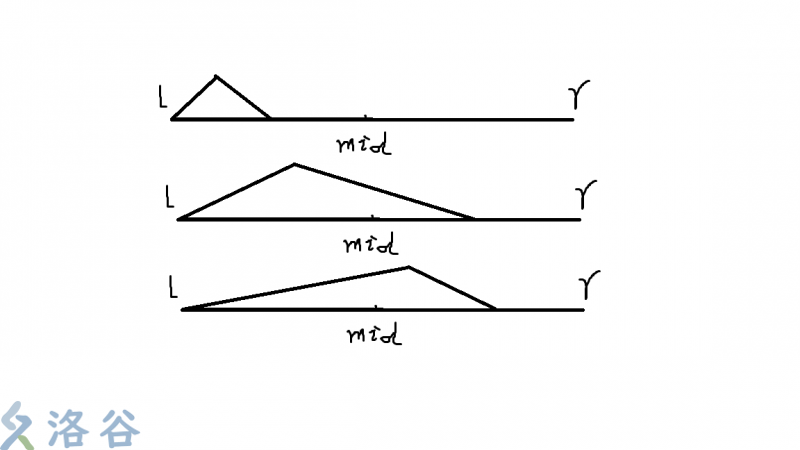
• 第一种情况就是左儿子的(zans)

• 第二种情况是左儿子的(zans+)右儿子中以左端点开始的最长下降序列长度（左儿子的右端点(>)右儿子的左端点）

• 第三种情况是左儿子的区间长度(+)右儿子的(zans)（左儿子中以右端点结尾的最长上升序列长度(=)左儿子的区间长度并且左儿子的右端点(<)右儿子的左端点）

• 然后是维护左右端点开始或结束的最长下降或上升的序列长度(zlen,ylen)，以(zlen)来说

• 第一种情况是左儿子的(zlen)
• 第二种情况是左儿子的(zlen+)右儿子的(zlen)（左儿子的(zlen=)左儿子的区间长度并且左儿子的右端点(>)右儿子的左端点）

然后这道题就做完啦

我们整理一下刚才要维护的东西

• 答案(ans)

• 左端点(z)

• 右端点(y)

• 区间长度(len)

• 左端点开始的答案(zans)

• 左端点开始的最长下降序列长度(zlen)

• 右端点结束的答案(yans)

• 右端点结束的最长上升序列长度(ylen)

至于区间加的操作，对于一个子树而言只影响左右端点，所以正常的打标记下放就可以了

Code

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
#define N 300000
#define zrt k << 1
#define yrt k << 1 | 1
using namespace std;
int n,m,a[N + 5];
struct node
{
    int ans,za,ya,zl,yl,len;
    long long z,y,tag;
};
struct Seg
{
    node s[N * 4 + 5];
    node upd(node x,node y)
    {
        node k;
        k.len = x.len + y.len;
        k.z = x.z;
        k.y = y.y;
        k.zl = x.zl;
        if (x.zl == x.len && x.y > y.z)
            k.zl += y.zl;
        k.yl = y.yl;
        if (y.yl == y.len && x.y < y.z)
            k.yl += x.yl;
        k.za = x.za;
        if (k.za == x.len && x.y > y.z)
            k.za += y.zl;
        if (x.yl == x.len && x.y < y.z)
            k.za = max(k.za,x.yl + y.za);
        k.ya = y.ya;
        if (k.ya == y.len && x.y < y.z)
            k.ya += x.yl;
        if (y.zl == y.len && x.y > y.z)
            k.ya = max(k.ya,y.zl + x.ya);
        k.ans = max(x.ans,y.ans);
        if (x.y > y.z)
            k.ans = max(k.ans,x.ya + y.zl);
        if (x.y < y.z)
            k.ans = max(k.ans,y.za + x.yl);
        return k;
    }
    void build(int k,int l,int r)
    {
        if (l == r)
        {
            s[k].ans = 1;
            s[k].ya = 1;
            s[k].za = 1;
            s[k].zl = 1;
            s[k].yl = 1;
            s[k].z = (long long)a[l];
            s[k].y = (long long)a[l];
            s[k].len = 1;
            return;
        }
        int mid = l + r >> 1;
        build(zrt,l,mid);
        build(yrt,mid + 1,r);
        s[k] = upd(s[zrt],s[yrt]);
    }
    void jia(int k,int l,int r,long long z)
    {
        s[k].z += z;
        s[k].y += z;
        s[k].tag += z;
    }
    void pushdown(int k,int l,int r,int mid)
    {
        if (!s[k].tag)
            return;
        jia(zrt,l,mid,s[k].tag);
        jia(yrt,mid + 1,r,s[k].tag);
        s[k].tag = 0;
    }
    void add(int k,int l,int r,int x,int y,long long z)
    {
        if (l >= x && r <= y)
        {
            jia(k,l,r,z);
            return;
        }
        int mid = l + r >> 1;
        pushdown(k,l,r,mid);
        if (x > mid)
            add(yrt,mid + 1,r,x,y,z);
        else
            if (y <= mid)
                add(zrt,l,mid,x,y,z);
            else
                add(zrt,l,mid,x,y,z),add(yrt,mid + 1,r,x,y,z);
        s[k] = upd(s[zrt],s[yrt]);
    }
}tree;
int main()
{
    scanf("%d",&n);
    for (int i = 1;i <= n;i++)
        scanf("%d",&a[i]);
    tree.build(1,1,n);
    scanf("%d",&m);
    int l,r;
    long long z;
    for (int i = 1;i <= m;i++)
    {
        scanf("%d%d%lld",&l,&r,&z);
        tree.add(1,1,n,l,r,z);
        printf("%d
",tree.s[1].ans);
    }
    return 0;
}