给定两个长度为 (n) 的正整数序列 ({a_i}) 与 ({b_i}),序列的下标为 (1, 2, cdots , n)。现在你需要分别对两个序列各指定恰好 (K) 个下标,要求至少有 (L) 个下标在两个序列中都被指定,使得这 (2K) 个下标在序列中对应的元素的总和最大。
形式化地说,你需要确定两个长度为 (K) 的序列 ({c_i}, {d_i}),其中
(1 leq c_1< c_2 < cdots < c_K leq n , 1 leq d_1 < d_2 < cdots < d_K leq n)
并要求 ({c_1, c_2, cdots , c_K} cap {d_1, d_2, · · · , d_K}geq L)
目标是最大化 (sum^{K}_{i=1} a_{c_i} +sum^{K}_{i=1} b_{d_i})
牛逼的贪心。
考虑比较暴力的做法,我们可以建如下的图。
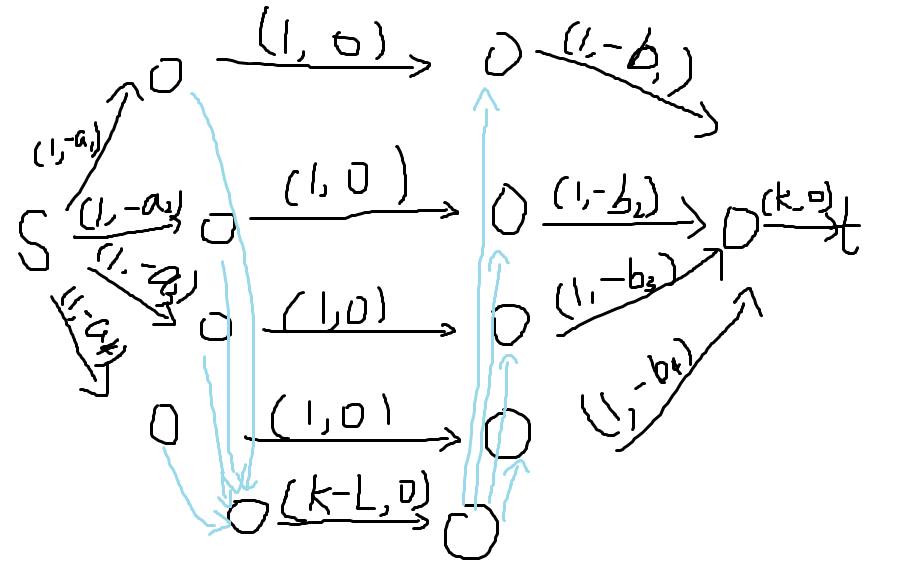
每个边上第一个数是流量,第二个数是费用,中间((1,0))的黑边代表选择下标相同的数,浅蓝色的边代表最多可以选(K-L)个下标不同的数,最后连向(t)的是最多选(K)个数。
然后在这个图上跑最小费用最大流就可以得到答案。
如何优化复杂度,考虑模拟费用流,首先(K-L)这条边的流比较好模拟,因为是随便选,所以考虑选(a,b)中前(K-L)大的数,然后如果选到下标相同的数,那么就不流这条,让他在对应的边中流是最优的。
我们选完之后就要考虑如何流对应的边,那么我们可以选择(a_i,b_i)都没被选过的流过去;还可以选择一个(a_i)被选过了,选一个(b_i)补上(a_i),然后(K-L)这条边少了一点流量,所以再选一个最大的没有被选的(a_i)来作为独立的来补充流量;(b_i)也是同理。
所以我们贪心地找最优的流法往后流,这样一定是最优的,因为每次都只会让对应的流量增加1,所以贪心显然正确。
然后有一点需要注意,就是如果(K-L)这条边的流量不满,那么我们一定要每次选(a,b)中各最大的来补充流量,比如这样子:
加了括号的是被选过了。
假设我们下一次选(a_3,b_2),那么(K-L)的流量就会不满,所以我们要在剩下的局面中各选一个最大的(a,b),假如是(a_5,b_1),这样就满足满流了,但如果最大的(a,b)是(a_5,b_5),那就还得继续选直到满流。
Code
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <queue>
#define mp make_pair
#define fi first
#define se second
const int N = 2e5;
long long inf = 1e17;
using namespace std;
int T,n,K,L,a[N + 5],b[N + 5],va[N + 5],vb[N + 5],ll,kk;
priority_queue <pair<int,int> > q,qa,qb,qqa,qqb;
long long ans,res;
int main()
{
scanf("%d",&T);
while (T--)
{
scanf("%d%d%d",&n,&K,&L);
for (int i = 1;i <= n;i++)
scanf("%d",&a[i]);
for (int i = 1;i <= n;i++)
scanf("%d",&b[i]);
for (int i = 1;i <= n;i++)
va[i] = vb[i] = 0;
ans = 0;
while (!q.empty())
q.pop();
while (!qa.empty())
qa.pop();
while (!qb.empty())
qb.pop();
for (int i = 1;i <= n;i++)
{
qa.push(mp(a[i],i));
qb.push(mp(b[i],i));
}
ll = 0;
for (int i = 1;i <= K && ll / 2 < K - L;i++)
{
if (qa.empty())
break;
int ua = qa.top().se,ub = qb.top().se;
qa.pop();qb.pop();
if (ua == ub)
continue;
if (vb[ua])
ll--,ans -= b[ua],vb[ua] = 0;
else
ll++,ans += a[ua],va[ua] = 1;
if (va[ub])
ll--,ans -= a[ub],va[ub] = 0;
else
ll++,ans += b[ub],vb[ub] = 1;
}
while (!qa.empty())
qa.pop();
while (!qb.empty())
qb.pop();
while (!qqa.empty())
qqa.pop();
while (!qqb.empty())
qqb.pop();
for (int i = 1;i <= n;i++)
{
if (!va[i] && vb[i])
qa.push(mp(a[i],i));
if (!vb[i] && va[i])
qb.push(mp(b[i],i));
if (!va[i] && !vb[i])
q.push(mp(a[i] + b[i],i));
if (!va[i])
qqa.push(mp(a[i],i));
if (!vb[i])
qqb.push(mp(b[i],i));
}
int mx = 0,typ = 0,ub,ua;
for (int i = 1;i <= K - ll / 2;i++)
{
mx = 0;
while (!q.empty() && (va[q.top().se] || vb[q.top().se]))
q.pop();
if (!q.empty())
{
if (mx < q.top().fi)
mx = q.top().fi,typ = 1;
}
while (!qa.empty() && va[qa.top().se])
qa.pop();
if (!qa.empty())
{
while (vb[qqb.top().se])
qqb.pop();
ub = qqb.top().se;
if (mx < qa.top().fi + b[ub])
mx = qa.top().fi + b[ub],typ = 2;
}
while (!qb.empty() && vb[qb.top().se])
qb.pop();
if (!qb.empty())
{
while (va[qqa.top().se])
qqa.pop();
ua = qqa.top().se;
if (mx < qb.top().fi + a[ua])
mx = qb.top().fi + a[ua],typ = 3;
}
ans += mx;
if (typ == 1)
{
va[q.top().se] = vb[q.top().se] = 1;
q.pop();
}
if (typ == 2)
{
ua = qa.top().se;
va[qa.top().se] = 1;
qa.pop();
vb[ub] = 1;
qqb.pop();
if (!va[ub])
qa.push(mp(a[ub],ub));
else
{
int sm = 1;
while (i != K - ll / 2 && sm)
{
sm--;
while (vb[qqb.top().se])
qqb.pop();
while (va[qqa.top().se])
qqa.pop();
ua = qqa.top().se,ub = qqb.top().se;
qqa.pop(),qqb.pop();
ans += a[ua] + b[ub];
va[ua] = vb[ub] = 1;
if (!vb[ua])
qb.push(mp(b[ua],ua));
else
sm++;
if (!va[ub])
qa.push(mp(a[ub],ub));
else
sm++;
i++;
}
}
}
if (typ == 3)
{
ub = qb.top().se;
vb[qb.top().se] = 1;
qb.pop();
va[ua] = 1;
qqa.pop();
if (!vb[ua])
qb.push(mp(b[ua],ua));
else
{
int sm = 1;
while (i != K - ll / 2 && sm)
{
sm--;
while (vb[qqb.top().se])
qqb.pop();
while (va[qqa.top().se])
qqa.pop();
ua = qqa.top().se,ub = qqb.top().se;
qqa.pop(),qqb.pop();
ans += a[ua] + b[ub];
va[ua] = vb[ub] = 1;
if (!vb[ua])
qb.push(mp(b[ua],ua));
else
sm++;
if (!va[ub])
qa.push(mp(a[ub],ub));
else
sm++;
i++;
}
}
}
}
cout<<ans<<endl;
}
return 0;
}