(Ciel) 某天兴致勃勃地找 (Juro) 玩起了一种卡牌游戏。每张卡牌有类型(攻击或防御)和力量值两个信息。
(Juro) 有 (n) 张卡牌,(Ciel) 有 (m) 张卡牌。已知 (Ciel) 的卡牌全是攻击型的。
游戏的每一轮都由 (Ciel) 进行操作,首先从自己手上选择一张没有使用过的卡牌X。
如果 (Juro) 手上没有卡牌,受到的伤害为 X 的力量值,否则 (Ciel) 要从 (Juro) 的手上选择一张卡牌 Y
。
若 Y 是攻击型(当 X 的力量值不小于 Y 的力量值时才可选择),此轮结束后 Y 消失,(Juro) 受到的伤害为 X 的力量值与 Y 的力量值的差;若 Y 是防御型(当 X 的力量值大于 Y 的力量值时才可选择),此轮结束后 Y 消失,(Juro) 不受到伤害。
(Ciel) 可以随时结束自己的操作(卡牌不一定要用完)。她想使得 (Juro) 受到的总伤害最大。你知道自己要做什么了吗?
(1le n,mle100,0le X,Yle8000)
好多做法啊,来一发费用流吧QAQ
对于这个题,我们会发现几个比较特殊的点:
-
(Ciel)可以选择随时结束操作。
-
当(Juro)没有牌之后,(Ciel)可以把自己剩下的牌全打上去。
第一个操作考虑直接枚举打了几张牌,多建一个点连向源点限制流量就可以。
重点是第二个操作,可以考虑把(Juro)的牌拆成两个点(i,i')。
-
(i o i')流量(1),费用(-2inf);
-
(i o T'),流量(1),费用(0);
用(j)表示(Ciel)的牌。
-
(S o j),流量(1),费用(0);
-
(j o i(k_i=ATK,X_jle Y_i)),流量(1),费用(inf-(X_j-Y_i));
-
(j o i(k_i=DEF,X_j>Y_i)),流量(1),费用(inf);
-
(j o T),流量(1),费用(inf-X_j)。
这样子为什么是对的?
注意那条费用为(-2inf)的边,因为我们跑最小费用最大流,所以我们肯定会优先流完那些边,才会流(inf-X_j)的边,这样子保证了先把(Juro)的牌打完才能打剩下的牌。
而我们之前多枚举了打几张牌(x),所以我们可以很容易通过最小费用还原伤害,最后建个这样的边:
- (SS o S),流量(x),费用(0)。
画出图来就是这样子的:
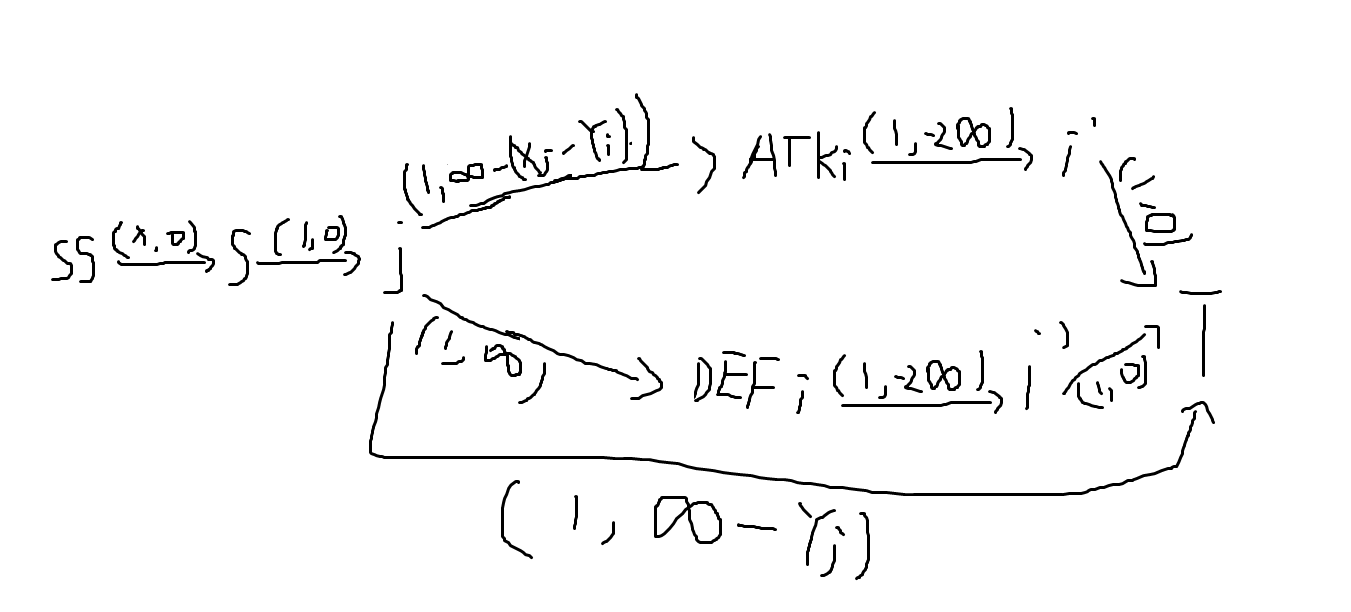
Code
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>
const int N = 100;
const int M = 1e6;
const int inf = 1e7;
const int INF = 2e9;
using namespace std;
struct card
{
int typ,v;
}a[N + 5];
int n,m,b[N + 5],s,ss,t,nxt[M * 2 + 5],head[M + 5],edge_cnt = 1,chi,cost,ans,ress,cur[M + 5],dis[M + 5],vis[M + 5],p[M + 5],q[M + 5];
struct edges
{
int v,w,f;
}edge[M * 2 + 5],e[M * 2 + 5];
char ch[10];
void add_edge(int u,int v,int w,int f)
{
edge[++edge_cnt] = (edges){v,w,f};
nxt[edge_cnt] = head[u];
head[u] = edge_cnt;
}
bool spfa(int s,int t)
{
for (int i = 1;i <= t;i++)
{
cur[i] = head[i];
dis[i] = INF;
p[i] = 0;
vis[i] = 0;
}
int l = 1,r = 0;
dis[s] = 0;
q[++r] = s;
vis[s] = 1;
while (l <= r)
{
int u = q[l++];
vis[u] = 0;
for (int i = head[u];i;i = nxt[i])
{
int v = edge[i].v,w = edge[i].w,f = edge[i].f;
if (dis[u] + f < dis[v] && w)
{
dis[v] = dis[u] + f;
if (!vis[v])
{
vis[v] = 1;
q[++r] = v;
}
}
}
}
return dis[t] != INF;
}
int dfs(int u,int flow)
{
if (u == t)
return flow;
int sm = 0;
p[u] = 1;
for (int &i = cur[u];i;i = nxt[i])
{
int v = edge[i].v,&w = edge[i].w,f = edge[i].f;
if (dis[u] + f == dis[v] && w && !p[v])
{
int res = dfs(v,min(w,flow));
w -= res;
sm += res;
flow -= res;
edge[i ^ 1].w += res;
cost += f * res;
if (!flow)
break;
}
}
return sm;
}
int main()
{
scanf("%d%d",&n,&m);
for (int i = 1;i <= n;i++)
{
scanf("%s",ch + 1);
scanf("%d",&a[i].v);
if (ch[1] == 'A')
a[i].typ = 1;
else
a[i].typ = 2;
}
for (int i = 1;i <= m;i++)
scanf("%d",&b[i]);
s = n * 2 + m + 1,ss = n * 2 + m + 2,t = n * 2 + m + 3;
for (int i = 1;i <= m;i++)
{
add_edge(ss,n * 2 + i,1,0);
add_edge(n * 2 + i,ss,0,0);
add_edge(n * 2 + i,t,1,inf - b[i]);
add_edge(t,n * 2 + i,0,b[i] - inf);
}
for (int i = 1;i <= n;i++)
{
add_edge(i,i + n,1,-2 * inf);
add_edge(i + n,i,0,2 * inf);
add_edge(i + n,t,1,0);
add_edge(t,i + n,0,0);
for (int j = 1;j <= m;j++)
{
if (a[i].typ == 1 && b[j] >= a[i].v)
{
add_edge(n * 2 + j,i,1,inf - (b[j] - a[i].v));
add_edge(i,n * 2 + j,0,b[j] - a[i].v - inf);
}
if (a[i].typ == 2 && b[j] > a[i].v)
{
add_edge(n * 2 + j,i,1,inf);
add_edge(i,n * 2 + j,0,-inf);
}
}
}
add_edge(s,ss,0,0);
chi = edge_cnt;
add_edge(ss,s,0,0);
for (int i = 2;i <= edge_cnt;i++)
e[i] = edge[i];
for (int i = 1;i <= m;i++)
{
e[chi].w = i;
for (int j = 2;j <= edge_cnt;j++)
edge[j] = e[j];
cost = 0;
while (spfa(s,t))
ress += dfs(s,inf);
//cout<<i<<" "<<cost<<" "<<-(inf * min(n,i) - inf * max(i - n,0) + cost)<<endl;
ans = max(ans,-(inf * min(n,i) - inf * max(i - n,0) + cost));
}
cout<<ans<<endl;
return 0;
}