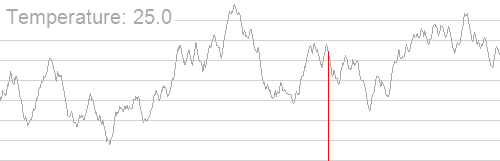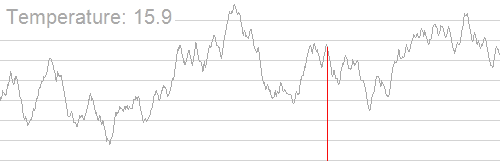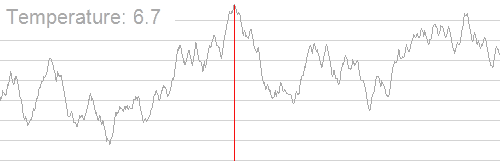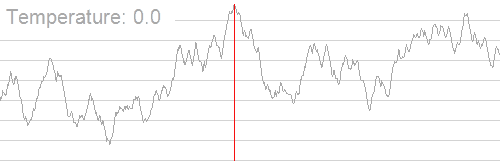
如图所示。
退火算法,爬山算法都是一种复杂度低,但是能得到近似解的算法。
其中爬山算法其实就是梯度下降,可能会陷入局部最优。
- 爬山算法:兔子朝着比现在高的地方跳去。它找到了不远处的最高山峰。但是这座山不一定是珠穆朗玛峰。这就是爬山算法,它不能保证局部最优值就是全局最优值。
- 模拟退火:兔子喝醉了。它随机地跳了很长时间。这期间,它可能走向高处,也可能踏入平地。但是,它渐渐清醒了并朝最高方向跳去。这就是模拟退火。
根据热力学规律并结合计算机对离散数据的处理, 我们定义: 如果当前温度为 (T), 当前状态与新状态之间的能量差为 (ΔE), 则发生状态转移的概率为:
[P(Delta E) = e^{dfrac {Delta E} {T}}
]
当 (Delta E) 为正的时候一定是转移成功的,对于 $Delta E < 0 $ , 则通过计算的概率接受这个新的解
可以写出如下一段伪代码
void mnth(){ //模拟退火...
for(double T = 初始温度;T > 终止温度;T *= 系数){
rand_operate();//做一个随机操作
now = cal(); //计算目前的答案
if(now < ans) ans = now;//若更优,直接转移
else if(exp((ans - now) / T) * RAND_MAX < rand()){
//这里写的是小于号,是不转移
//不转移,撤销刚刚的随机操作
}
}
}
看两道题
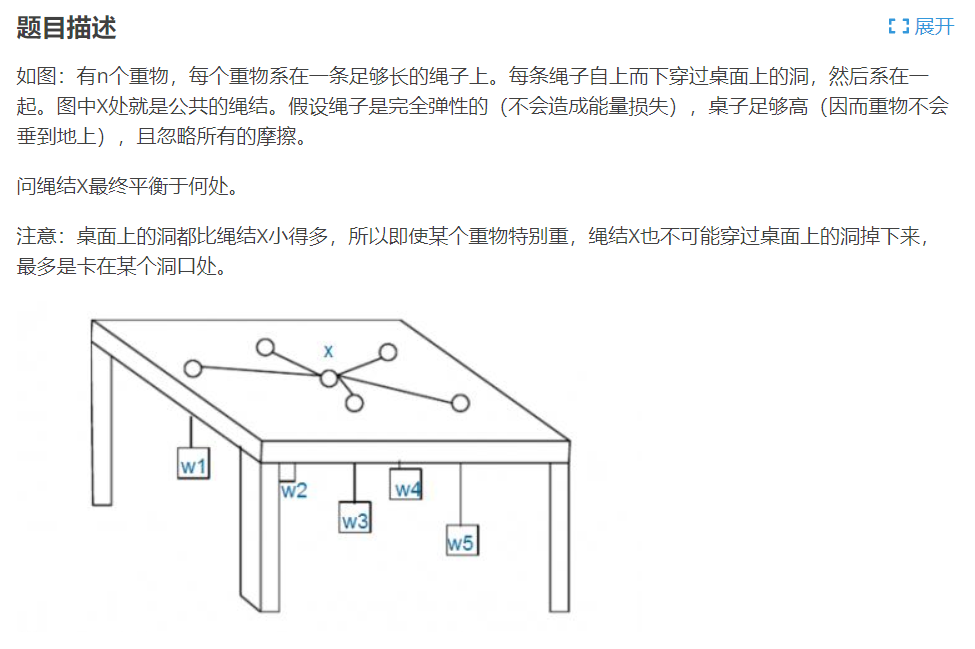
其实就是选一个点,使得这个点到所有点的距离乘上质量之和要最小
相当于在二维的平面找一个最优解
#include<bits/stdc++.h>
#define N 2000
using namespace std;
struct node
{
double x, y, w;
}e[N];
int n;
double ansx, ansy;
const double eps = 1e-15;
double f(double x, double y)
{
double tot = 0;
for (int i = 1; i <= n; i++){
double delx = x - e[i].x;
double dely = y - e[i].y;
tot += sqrt(delx * delx + dely * dely) * e[i].w;
}
return tot;
}
void mnth()
{
for(double T = 5000;T > 1e-15;T *= 0.995){
double nowx = ansx + (rand() * 2 - RAND_MAX) * T;
double nowy = ansy + (rand() * 2 - RAND_MAX) * T;
double delta = f(nowx, nowy) - f(ansx, ansy);
if (delta < 0)ansx = nowx, ansy = nowy;
else if (exp(-delta / T)> rand()*1.0/RAND_MAX)ansx = nowx, ansy = nowy;
}
}
int main(){
scanf("%d", &n);
for (int i = 1; i <= n; i++){
scanf("%lf%lf%lf", &e[i].x, &e[i].y, &e[i].w);
ansx += e[i].x; ansy += e[i].y;
}
ansx /= (double)n; ansy /= (double)n;
mnth();
printf("%.3lf %.3lf
", ansx, ansy);
}
现在有 (n) 枚金币,它们可能会有不同的价值,第 (i) 枚金币的价值为 (v_i) 。
现在要把它们分成两部分,要求这两部分金币数目之差不超过 1 ,问这样分成的两部分金币的价值之差最小是多少?
每次随机交换两个元素
当时这里的小于号和大于号弄混了,调了好久
#include<bits/stdc++.h>
using namespace std;
int ans, T, n, A[50];
int get() {
int sum = 0;
for (int i = 0; i < n; i++) {
if (i < n / 2)sum += A[i];
else sum -= A[i];
}
return abs(sum);
}
void mnth() {
for (double T = 5000; T > 1e-15; T *= 0.945) {
int x = rand() % n, y = rand() % n;
swap(A[x], A[y]); int now = get();
if (now < ans) ans = now;
else if (exp((ans - now) / T) * RAND_MAX < rand()) swap(A[x], A[y]); // > 是转移, < 是撤销
}
}
int main() {
scanf("%d", &T);
while (T--) {
scanf("%d", &n);
for (int i = 0; i < n; i++)scanf("%d", A + i);
ans = 0x7fffffff; int x = 1000; while (x--)mnth();
printf("%d
", ans);
}
}