动态树LCT（Link-Cut-Tree）

(LCT) 可以动态维护一个森林

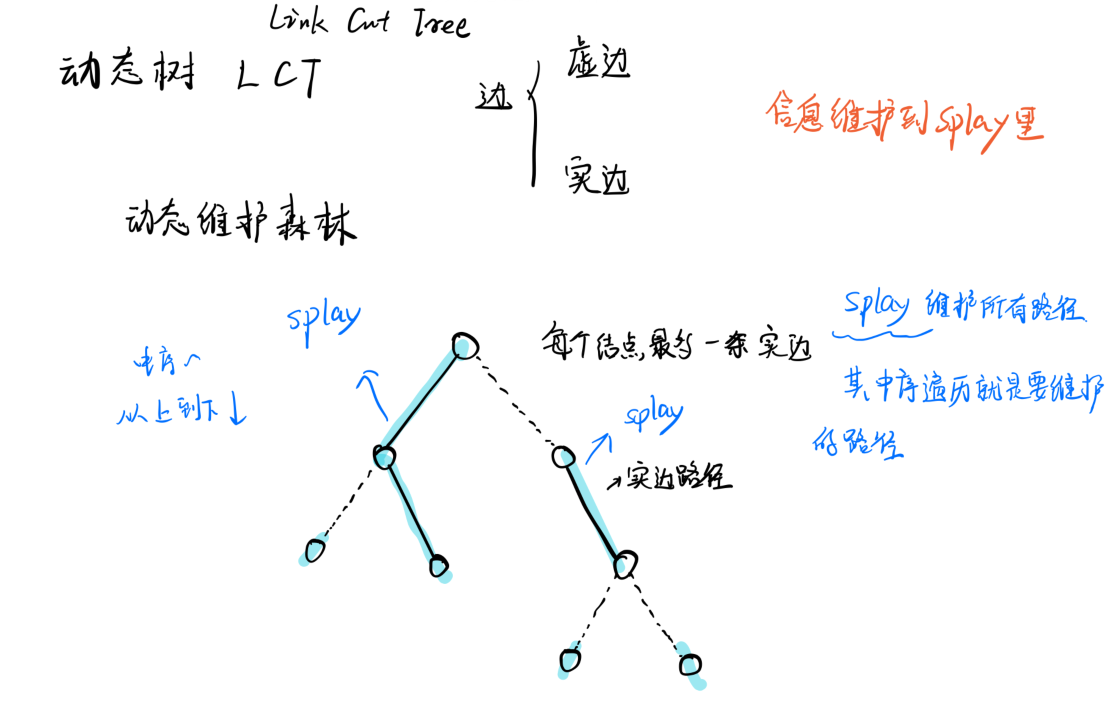
每个节点最多只能连接一条实边 ，被父亲节点指向的实边不属于自己的实边。

实边和虚边是维护的一种方式，实边和虚边在原图中都是真实存在的边。

一棵树中的实边和虚边可以相互变换

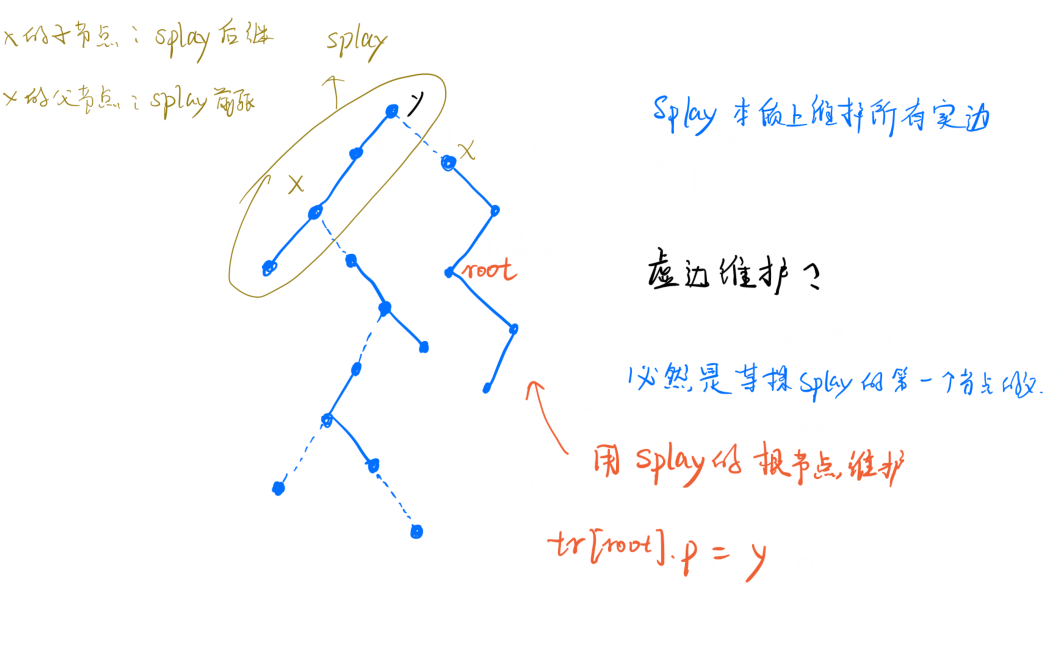
用 (Splay) 维护所有的实边

LCT 的基本操作

Access(x)

将 (x) 所在的树的根节点与 (x) 之间的路径变成实边路径

并且将 (x) 旋转至该实边路径 (Splay) 的根节点

不改变原树的结构

make_root(x)

将 (x) 变成根节点，这个根节点指的是原树的根节点

find_root(x)

找到 (x) 所在树的根节点

将根节点与 (x) 之间的路径变成实边路径，并且将 原树的根节点 旋转到 (Splay) 的根节点

split(x,y)

将 (x) 和 (y) 建立一条实边路径

先连通根节点和 (x) 成为实体路径，然后将 (x) 变成根

然后连通根节点 (x) 和 (y)

link(x,y)

若 (x) , (y) 不连通，则建立一条虚边

cut(x,y)

若 (x) , (y) 存在边，则删除它

/*
 * @Author: zhl
 * @Date: 2020-11-20 15:08:50
 */

#include<bits/stdc++.h>
using namespace std;

const int N = 1e5 + 10;

int n, m;

struct node {
	int s[2], p, v;
	int sum, rev;
}tr[N];
int stk[N];


void rev(int x) {
	swap(tr[x].s[0], tr[x].s[1]);
	tr[x].rev ^= 1;
}

void push_up(int x) {
	tr[x].sum = tr[tr[x].s[0]].sum ^ tr[tr[x].s[1]].sum ^ tr[x].v;
}

void push_down(int x) {
	if (tr[x].rev) {
		rev(tr[x].s[0]); rev(tr[x].s[1]);
		tr[x].rev = 0;
	}
}

bool is_root(int x) {
	return tr[tr[x].p].s[0] != x and tr[tr[x].p].s[1] != x;
}

void rotate(int x) {
	int y = tr[x].p, z = tr[y].p;
	int k = tr[y].s[1] == x;
	if (!is_root(y)) tr[z].s[tr[z].s[1] == y] = x;
	tr[x].p = z;
	tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;
	tr[x].s[k ^ 1] = y; tr[y].p = x;
	push_up(y), push_up(x);
}

void splay(int x) {
	int top = 0, r = x;
	stk[++top] = r;
	while (!is_root(r)) stk[++top] = r = tr[r].p;
	while (top)push_down(stk[top--]); 

	while (!is_root(x)) {
		int y = tr[x].p, z = tr[y].p;
		if (!is_root(y)){
			if((tr[y].s[0] == x) ^ (tr[z].s[0] == y))rotate(x);
			else rotate(y);
		}
		rotate(x);
	}
}

void access(int x) {
	/*
		将 x 所在的树的根节点与 x 之间的路径变成实边路径
		并且将 x 旋转至该实边路径splay的根节点
	*/
	int z = x;
	for (int y = 0; x; y = x, x = tr[x].p) {
		splay(x);
		tr[x].s[1] = y, push_up(x);
	}
	splay(z);
}

void make_root(int x) {
	/*
		将 x 变成 x 所在树中的根节点
	*/
	access(x);
	rev(x);
}

int find_root(int x) {
	/*
		查询 x 所在树的根节点
		将根节点与 x 之间的路径变成实边路径，并且将 原树的根节点 旋转到splay的根节点
	*/
	access(x);
	while (tr[x].s[0])push_down(x), x = tr[x].s[0];
	splay(x);
	return x;      
}

void split(int x, int y) {
	/*
		将 x 和 y 建立一条实边路径
		先连通根节点和 x 成为实体路径，然后将 x 变成根
		然后连通根节点 x 和 y
	*/
	make_root(x);
	access(y);
}

void link(int x, int y) {
	/*
		若 x 和 y 不连通
		建立一虚边
	*/
	make_root(x);
	if (find_root(y) != x) tr[x].p = y;
}

void cut(int x, int y) {
	/*
		若 x， y 存在边
		则删除它
	*/
	make_root(x);
	if (find_root(y) == x and tr[y].p == x and !tr[y].s[0]) {
		tr[x].s[1] = tr[y].p = 0;
		push_up(x);
	}
}

int main() {
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= n; i++)scanf("%d", &tr[i].v);

	while (m--) {
		int t, x, y;
		scanf("%d%d%d", &t, &x, &y);
		if (t == 0) {
			split(x, y);
			printf("%d
", tr[y].sum);
		}
		else if (t == 1) link(x, y);
		else if (t == 2) cut(x, y);
		else {
			splay(x);
			tr[x].v = y;
			push_up(x);
		}
	}
}