左偏树（可并堆）

说是左偏树，其实叫可并堆更合理

对一个节点来说，它的左右子树的值都要大于它自己的值

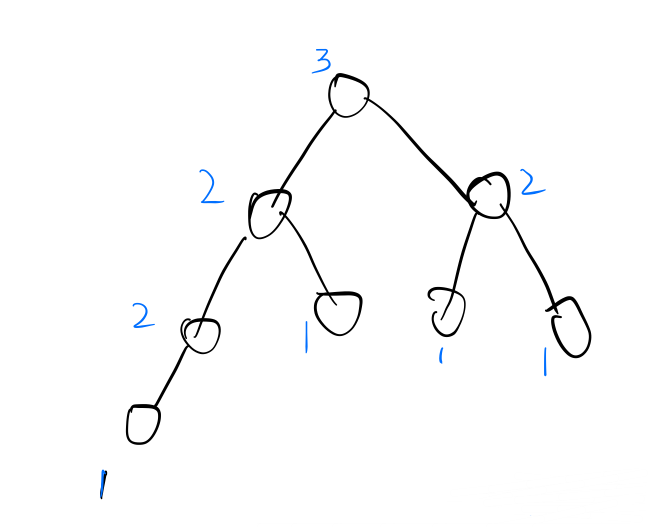
定义距离 (dis) : 每个节点到空节点的距离

左偏树有一个重要的性质：

• 每个子树的左儿子的 (dis) 要大于等于 右儿子的 (dis) ，所以直觉上来说就是

“左偏”

• 插入 : (O(log n))
• 求最小值： (O(1))
• 删除最小值： (O(log n))
• 合并两棵树： (O(log n))

P3377 【模板】左偏树（可并堆） - 洛谷

/*
 * @Author: zhl
 * @Date: 2020-11-21 11:16:27
 */
#include<bits/stdc++.h>
using namespace std;

const int N = 2e5 + 10;

int l[N], r[N], v[N], fa[N], idx, dis[N];

int find(int a) {
	return a == fa[a] ? a : fa[a] = find(fa[a]);
}
bool cmp(int a, int b) {
	if (v[a] != v[b])return v[a] < v[b];
	return a < b;
}
int merge(int a, int b) {
	if (!a or !b)return a + b;
	if (cmp(b, a))swap(a, b);
	r[a] = merge(r[a], b);
	if (dis[r[a]] > dis[l[a]])swap(l[a], r[a]);
	dis[a] = dis[r[a]] + 1;
	return a;
}
int n;
int main() {
	v[0] = 2e9;
	scanf("%d", &n);
	while (n--) {
		int op, a, b;
		scanf("%d%d", &op, &a);
		if (op == 1) {
			v[++idx] = a;
			dis[idx] = 1;
			fa[idx] = idx;
		}
		else if (op == 2) {
			scanf("%d", &b);
			a = find(a), b = find(b);
			if (a != b) {
				if (cmp(b, a)) swap(a, b);
				fa[b] = a;
				merge(a, b);
			}
		}
		else if (op == 3) {
			printf("%d
", v[find(a)]);
		}
		else {
			a = find(a);
			if (cmp(r[a], l[a]))swap(l[a], r[a]);
			fa[a] = l[a]; fa[l[a]] = l[a];
			merge(l[a], r[a]);
		}
	}
}