后缀数组可以求出一个串 (s) 的所有后缀的排名
有两种算法
倍增 : (O(nlogn)) 常数小
DC3 : (O(n)) 常数大
这里使用倍增就可以
在 (O(nlogn)) 的时间求出以下信息
sa数组,sa[i]表示排第i位的是第sa[i]个后缀
rk数组,rk[i]表示第i个后缀的排名是rk[i]
height[i]表示第sa[i]个后缀与sa[i-1]的最长公共前缀
如何倍增
首先把所有后缀按照第一个字母排序,使用 (O(n)) 的基数排序
假设已经按前 (k) 个字母排好序,下轮考虑前 (2k) 个字母
我们把前 (k) 个字母看作第一关键字, 后 (k) 个字母看作第二关键字
则只需要按照第二关键字排好序,然后再按第一关键字进行稳定的基数排序,就可以完成按照前 (2k) 个字母排序
我们发现,第 (i) 个后缀的第二关键字是第 (i + k) 个后缀的第一关键字
void get_sa() {
//先按照第一个字母排序
for (int i = 1; i <= n; i++) c[x[i] = s[i]] ++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1]; //小于等于i的数目
for (int i = n; i; i--) sa[c[x[i]] --] = i;
//开始倍增
for (int k = 1; k <= n; k <<= 1){
int num = 0;
for (int i = n - k + 1; i <= n; i++) y[++num] = i; //第二关键字是空串,肯定在最前面
for (int i = 1; i <= n; i++)
if (sa[i] > k)
y[++num] = sa[i] - k;
for (int i = 1; i <= m; i++) c[i] = 0;
for (int i = 1; i <= n; i++) c[x[i]] ++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
//按第二关键字倒序枚举
for (int i = n; i; i--) sa[c[x[y[i]]] --] = y[i], y[i] = 0;
swap(x, y); //把 x 暂时存到 y 中
//离散化
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i++)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;
if (num == n) break;
m = num;
}
}
如何求 height 数组
首先定义
(lcp(i,j)) 表示排名为 (i) 的后缀和排名为 (j) 的后缀的最长公共前缀长度
则显然有一下几条性质
- (lcp(i,j) = lcp(j,i))
- (lcp(i,i) = len(i))
还有一条如下的性质, 对于 $ i le k le j$
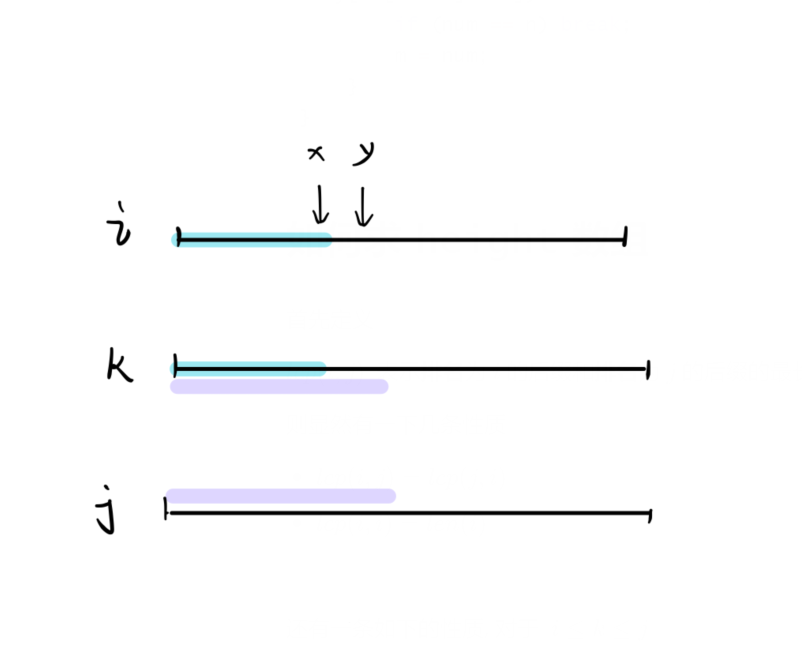
(i) 和 (j) 在 (y) 处的字符不会相等,若相等则 (lcp(i,k)) 可以继续扩展
由此可以推出
至此,我们来考虑 height 的求法
(height(i) = lcp(i-1,i))
设 (h(i) = height(rk[i])) , 第 (i) 个后缀与排名在它前一位的后缀的 (lcp)
我们考虑第 (i - 1) 个后缀,设第 (k) 个后缀是排名在它前一位的后缀
则
即
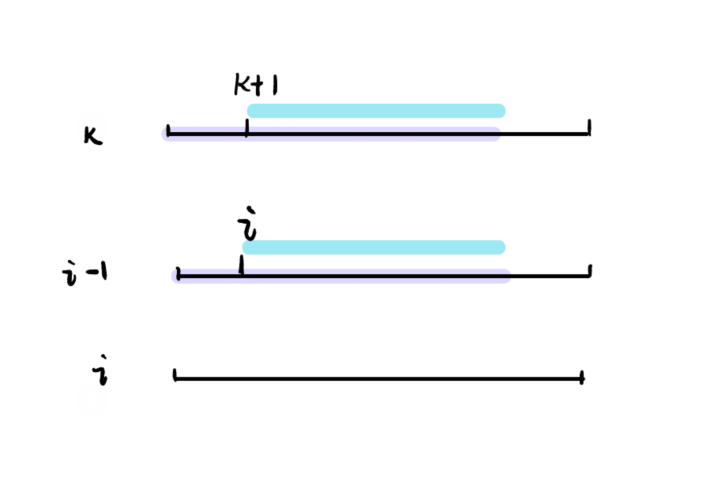
根据之前推的性质,排名在第 (i) 个后缀的前一位的后缀不妨在 (k) 之前,
有
有了这一条性质后,我们可以在 (O(n)) 时间内求出 height 数组
void get_height()
{
for (int i = 1; i <= n; i++) rk[sa[i]] = i;
for (int i = 1, k = 0; i <= n; i++)
{
if (rk[i] == 1) continue;
if (k) k--; //只需要从 h[i-1] - 1 开始枚举就可以
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
height[rk[i]] = k;
}
}
/*
* @Author: zhl
* @Date: 2020-11-24 10:30:50
*/
#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 10;
int n, m;
char s[N];
int sa[N], x[N], y[N], c[N], rk[N], height[N];
/*
sa[i] :
x[i] : 第一关键字
y[i] : 第二关键字
c[i] : 桶
rk[i] :
*/
void get_sa() {
for (int i = 1; i <= n; i++) c[x[i] = s[i]] ++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i; i--) sa[c[x[i]] --] = i; // sa[i] = k 表示 rank i 的串从 k 位置开始
for (int k = 1; k <= n; k <<= 1){
int num = 0;
for (int i = n - k + 1; i <= n; i++) y[++num] = i;
for (int i = 1; i <= n; i++)
if (sa[i] > k)
y[++num] = sa[i] - k;
for (int i = 1; i <= m; i++) c[i] = 0;
for (int i = 1; i <= n; i++) c[x[i]] ++;
for (int i = 2; i <= m; i++) c[i] += c[i - 1];
for (int i = n; i; i--) sa[c[x[y[i]]] --] = y[i], y[i] = 0;
swap(x, y); //把 x 暂时存到 y 中
//离散化
x[sa[1]] = 1, num = 1;
for (int i = 2; i <= n; i++)
x[sa[i]] = (y[sa[i]] == y[sa[i - 1]] && y[sa[i] + k] == y[sa[i - 1] + k]) ? num : ++num;
if (num == n) break;
m = num;
}
}
void get_height()
{
for (int i = 1; i <= n; i++) rk[sa[i]] = i;
for (int i = 1, k = 0; i <= n; i++)
{
if (rk[i] == 1) continue;
if (k) k--; //只需要从 h[i-1] - 1 开始枚举就可以
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
height[rk[i]] = k;
}
}
int main(){
scanf("%s", s + 1);
n = strlen(s + 1), m = 122;
get_sa();
//get_height();
for (int i = 1; i <= n; i++) printf("%d ", sa[i]);
puts("");
/*for (int i = 1; i <= n; i++) printf("%d ", height[i]);
puts("");*/
return 0;
}