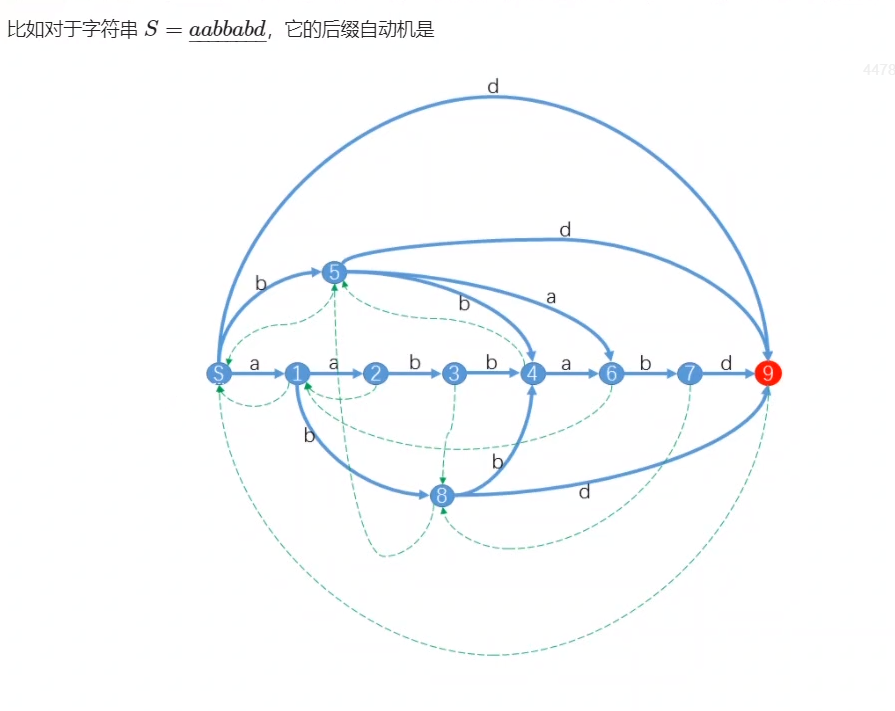
一、(SAM) 的性质:
(SAM) 是个状态机。一个起点,若干终点。原串的所有子串和从 (SAM) 起点开始的所有路径一一对应,不重不漏。所以终点就是包含后缀的点。
每个点包含若干子串,每个子串都一一对应一条从起点到该点的路径。且这些子串一定是里面最长子串的连续后缀。
(SAM) 问题中经常考虑两种边:
(1) 普通边,类似于 (Trie)。表示在某个状态所表示的所有子串的后面添加一个字符。
(2) (Link、Father)。表示将某个状态所表示的最短子串的首字母删除。这类边构成一棵树。
二、(SAM) 的构造思路
(endpos(s)):子串 (s) 所有出现的位置(尾字母下标)集合。(SAM) 中的每个状态都一一对应一个 (endpos) 的等价类。
(endpos) 的性质:
(1) 令 (s1,s2) 为 (S) 的两个子串 ,不妨设 (|s1|≤|s2|) (我们用 (|s|) 表示 (s) 的长度 ,此处等价于 (s1) 不长于 (s2) )。
则 (s1) 是 (s2) 的后缀当且仅当 (endpos(s1)⊇endpos(s2)) ,(s1) 不是 (s2) 的后缀当且仅当 en(dpos(s1)∩endpos(s2)=∅) 。
(2) 两个不同子串的 (endpos),要么有包含关系,要么没有交集。
(3) 两个子串的 (endpos) 相同,那么短串为长串的后缀。
(4) 对于一个状态 (st) ,以及任意的 (longest(st)) 的后缀 s ,如果 (s) 的长度满足:(|shortest(st)|≤|s|≤|longsest(st)| ,)那么 (s∈substrings(st)) 。
算法:

#include<bits/stdc++.h>
using namespace std;
const int N = 2e6 + 10;
struct Edge {
int to, next;
}E[N];
int head[N], cnt;
void addEdge(int from, int to) {
E[cnt] = { to,head[from] };
head[from] = cnt++;
}
int tot = 1, last = 1;
struct Node {
int len, fa;
int ch[26];
}node[N];
typedef long long ll;
char s[N];
ll f[N];
void extend(int c) {
int p = last, np = last = ++tot;
f[tot] = 1;
node[np].len = node[p].len + 1;
for (; p && !node[p].ch[c]; p = node[p].fa) node[p].ch[c] = np;
if (!p)node[np].fa = 1;
else {
int q = node[p].ch[c];
if (node[q].len == node[p].len + 1) node[np].fa = q;
else {
int nq = ++tot;
node[nq] = node[q], node[nq].len = node[p].len + 1;
node[q].fa = node[np].fa = nq;
for (; p and node[p].ch[c] == q; p = node[p].fa) node[p].ch[c] = nq;
}
}
}
ll ans;
void dfs(int u) {
for (int i = head[u]; ~i; i = E[i].next) {
dfs(E[i].to);
f[u] += f[E[i].to];
}
if (f[u] > 1) ans = max(ans, f[u] * node[u].len);
}
int main() {
scanf("%s", s);
for (int i = 0; s[i]; i++)extend(s[i] - 'a');
memset(head, -1, sizeof head);
for (int i = 2; i <= tot; i++) {
addEdge(node[i].fa, i);
}
dfs(1);
printf("%lld
", ans);
}