面向对象第三单元作业总结

一、JML语言及其工具链

1.1 JML语法总结

a)语言框架结构

单行：//@
多行：/*@  
             @  
             @*/
嵌入：/*@pure@*/

结构：/*@ public normal_behavior
       @ requires condition
       @ assignable 
       @ ensures 
       @ also 
       @ public exception_behavior
       @ requires condition
       @ signal exception (condition)
       @ signal_only() 
       @ */

 b) 关键字及其含义

        othing 表示无

        esult 表示返回结果

        forall 表示任意

        exsits 表示存在

        pure 表示此方法不会修改任何值

        public_spec 表示此属性或规格的公开的

        also 连接两个不同的行为

        requires 要求输入满足的条件

        ensures 返回结果保证的条件

        signal 跑出异常的行为

        invariant 不变量

        not_null 被修饰对象非空

c) 符号与元素

        &&/||/! 与/或/非

        !=/== 不等/相等

        ==> 蕴含

        int 表明一个整数

d) 其他

        和编程语言不同，允许使用连续的不等号表示范围，如0 < i < a.length。

        其他的描述和java基本相同。

1.2 JML工具链一览

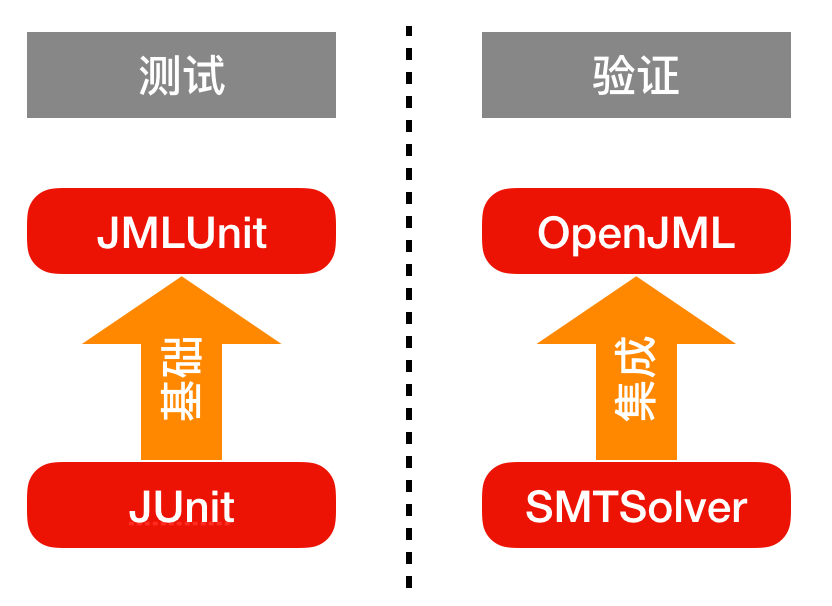
      本次作业一共使用了四个和JML相关的工具，OpenJML，JUnit，JMLUnitNG，SMT Solver。功能分别如下：

      JUnit：单元测试工具，可以对某一个类的特定方法进行测试。（严格来说这个和JML不直接相关，但是JML要依托JUnit进行测试）

      JMLUnitNG：可以自动生成测试用例进行JUnit测试。

      OpenJML：可以根据程序的规格进行静态和运行时检查，检查程序是否遵守了规格。

      SMT Solver：形式化验证工具，已经集成在了OpenJML里面。

      这四个工具可以进行一个大致的分类，JUnit和JMLUnitNG属于通过测试进行检查的工具，SMT Solver和OpenJML属于通过验证进行检查的工具。再考虑彼此的关系可以画出下图。

 

二、SMT Solver的部署与使用

2.1 SMT Solver的部署

      SMT Solver采用微软开源的Z3 SMT Solver。部署十分简单。前往github网址下载release版本即可。但是这个版本是一个命令行程序，考虑到OpenJML已经集成了SMT Solver，并且OpenJML也已经和IntelJ集成，所以直接使用OpenJML岂不是更好？

      不过在IntelJ上集成OpenJML有两个坑（也就是下面括号里的字）。集成步骤如下：

      step1 在IntelJ上安装了OpenJML/ESC插件（貌似只有IntelJ2018.3版本能够正确使用这个插件）

      step2 下载OpenJML/ESC，并在IntelJ中设置指定的路径。（注意这里的路径不能有空格，所以遇到空格需要反斜杠转义）

      step3 选择SMT Solver，我选了z3-4.7.1。

实在用不了，报错。。。 

三、JMLUnitNG部署与应用

3.1 JMLUnitNG的部署

谈不上部署，因为只是一个jar包，并需要和IntelJ集成。

3.2 针对Graph接口生成测试

step1  选择文件

 选取了MyPath.java文件，并进行了简化。

step2 生成测试文件

java -jar jmlunitng-1.4.jar MyPath.java

step3 编译测试文件

javac -cp jmlunitng-1_4.jar MyPath_JML_test.java

strp4 编译自己的文件

javac -cp jmlunitng-1_4.jar MyPath.java

step5 测试

java -cp jmlunitng-1_4.jar MyPath_JML_Test

结果如下：

 

 测试结果如下：

 

四、架构设计及其演化

4.1 三次作业的架构

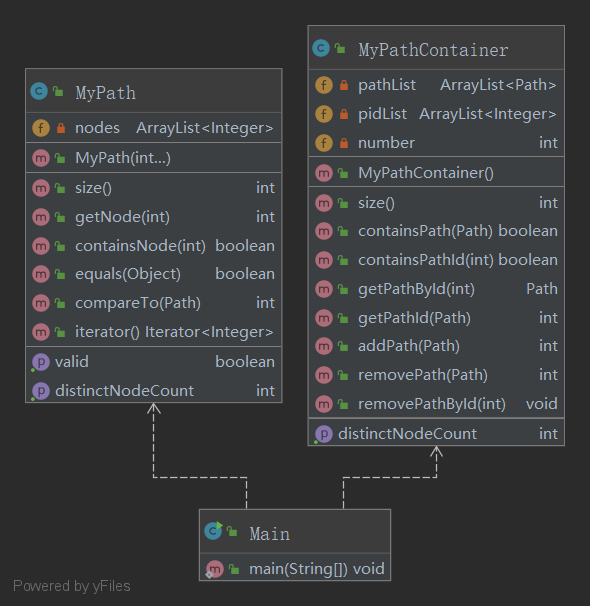
      三次作业的类图如下：

      第一次作业

      第二次作业

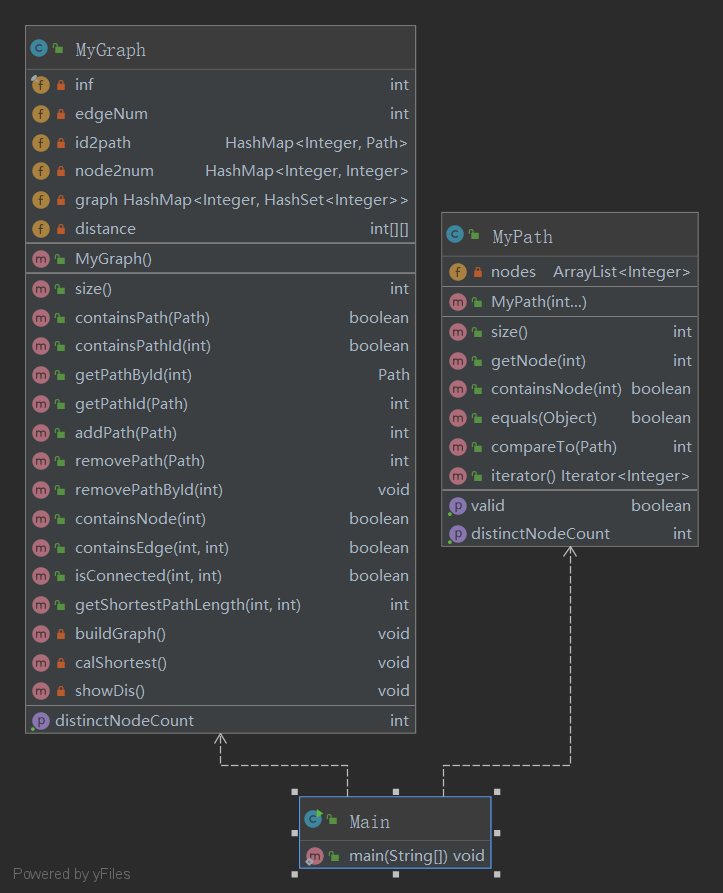
      第三次作业

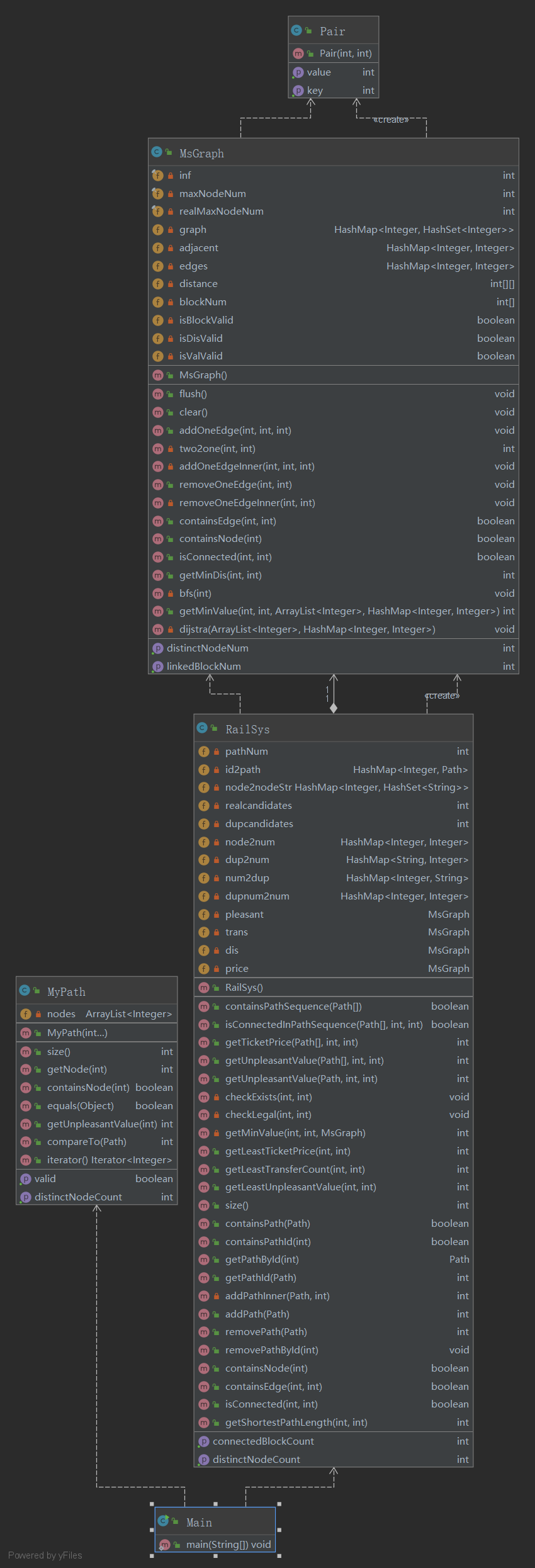
4.2 架构演化分析

      三次作业的整体架构几乎不变。除了第三次增加了两个类，其他的几乎不变。当然增加的两个类主要是服务RailwaySystem，所以耦合度并不高。

      Path类。三次演化中，Path类是几乎不变的，除了第二次意识到第一次每次都查一遍点导致超时所以增加了一个变量记录DistinctNode外，就没有更改过了。

      PathContainer/Graph/RailwaySystem类，这个类实现的方法在不断增加，从PathContainer到Graph，这两次作业之间的改动是很少的，只需要增加一些方法。之前实现的方法没有任何改动。

      但是从Graph到RailwaySystem架构发生了比较大的变化。新增了两个类，其中Pair类比较简单，其实使用javafx.util.Pair即可，但是考虑到jar包运行的问题，我自己实现了一个简单的Pair。另外一个类MsGraph，这是一个图类。这个类的主要作用是实现所有图相关的数据结构和算法，因为第三次作业中有很多不同类型的图。所以，此处的MsGraph的作用是纯粹的图类，所谓纯粹，是因为其中任何的数据结构都不和本次问题发生关系，所有的节点和边都是抽象的。而RailwaySystem类则主要实现用户输入到这张纯粹图的映射，为图类屏蔽问题的差异。所以，其实第三次作业中，MsGraph才是Graph的演化，（BTW，Ms是My super的意思），MsGraph是在第二次实现的图类基础上增加了迪杰斯特拉方法求最短路产生的。而RailwaySystem则主要是建立各种索引让各个图相互配合，完成功能。

五、Bug分析

5.1 使用Junit进行单元测试

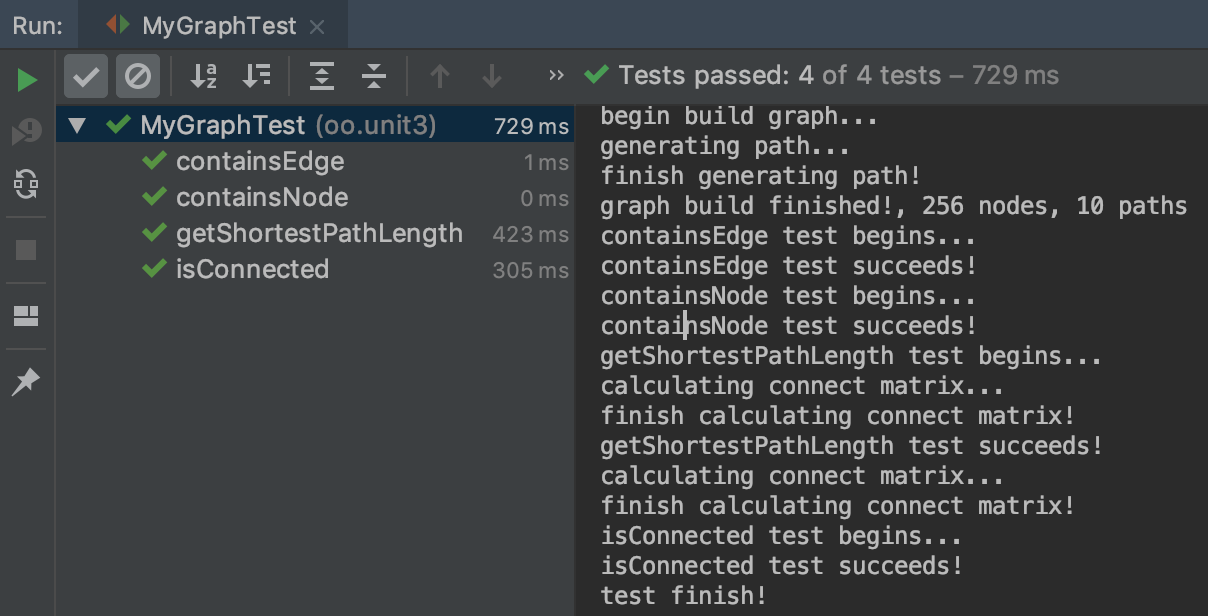
      不同的方法测试难度并不一样，容易测试的方法一般有两个特征，一是返回值可能的数量少比如布尔类型的方法，一种是逻辑比较简单没有算法比如增删路径。这些比较容易测试的方法主要是isConnected, CONTAINS_*以及addPath之类，可以用Junit进行单元测试，构造几个用例就基本有信心保证正确性。以下是第二次作业图类测试部分Junit测试代码。

public class MyGraphTest {
    //相关属性的定义  此处省略

    @BeforeClass
    public static void setG() {
        // 构造图的准备工作 省略
    }
    @Test
    public void containsNode() {
        System.out.println("containsNode test begins...");
        for (Integer node: allNodes) {
            try {
                assert (g.containsNode(node));
            } catch (AssertionError e) {
                System.out.println("ERROR: " + node + " not contain");
                continue;
            }
        }
        System.out.println("containsNode test succeeds!");
    }

    @Test
    public void containsEdge() {
        System.out.println("containsEdge test begins...");
        for (Path p: ps) {
            for (int i = 1; i < p.size(); i++) {
                assert (g.containsEdge(p.getNode(i-1), p.getNode(i)));
            }
        }
        System.out.println("containsEdge test succeeds!");
    }

    @Test
    public void isConnected() {
        cal_connect();
        if (distance == null) {
            distance = floyd();
        }
        System.out.println("isConnected test begins...");
        for (Integer fromNode: allNodes) {
            for (Integer toNode: allNodes) {
                try {
                    if (distance[node2num.get(fromNode)][node2num.get(toNode)] == 0) {
                        assert (fromNode == toNode);
                    } else if (distance[node2num.get(fromNode)][node2num.get(toNode)] != inf) {
                        assert (g.isConnected(fromNode, toNode));
                    } else {
                        assert (!g.isConnected(fromNode, toNode));
                    }
                } catch (NodeIdNotFoundException e) {
                    e.printStackTrace();
                }
            }
        }
        System.out.println("isConnected test succeeds!");
    }

    @Test
    public void getShortestPathLength() {
        System.out.println("getShortestPathLength test begins...");
        cal_connect();
        int[][] answer = floyd();
        //采用出错率较低的floyd进行对拍，此处省略
        }
        System.out.println("getShortestPathLength test succeeds!");
    }
    @AfterClass
    public static void finish() {
        System.out.println("test finish!");
    }

}

      测试结果如下：

 

5.2 Corner Case测试

      对于路径中有诸多平行边，起点和终点一致的查询等等corner case进行测试。比如：

PATH_ADD 1 2 2

CONTAINS_EDGE 2 2

PATH_ADD 1 2 2 2 3

PATH_REMOVE 1 2 2

CONTAINS_EDGE 2 2

      诸如此类的corner case还有很多，经过测试后都没有问题。但是这样的测试极为有限，而且并不能保证正确性。

5.3 搭建对拍框架进行多人对拍

      还有一些方法并不容易测试，比如最短距离等等，即使是写一个对拍程序，对拍程序本身的正确性也不易保证。此外各个方法之间的综合作用是否会出问题也不容易使用Junit测试。所以必须进行整合测试。但是这次作业不像电梯，电梯可以有一个另外的逻辑推断结果的合理性，但是这次测试并没有。可是我们又没有标程，为此只能通过群体智慧进行测试。随机生成测试用例后，运行若干同学的jar包，然后把结果进行比对。如果大家输出的结果都一样，那么就有比较大的把握认为程序是正确的，如果有一个人和其他人都不一样，那大概率是这个人错了。

      我搭建了一个多人对拍框架，它具有以下几个特征：

      1 并发测试：同时运行多组java进程进行测试提高测试效率。采用python线程池，每个python线程开启一个新的Java进程。

def run(jar, input_file):
    cmdLine = "cat " + os.path.join(TEST_DIR, input_file) + " | (time java -jar " + os.path.join(JAR_DIR, jar) + ")"
    path_name = input_file.split(".")[0]
    num = path_name.split('/')[-1]
    num = num[1:]
    res = subprocess.getoutput(cmdLine)
    des = os.path.join(OUT_DIR, num + jar.split('.')[0]) + ".txt"
    f = open(des, "w")
    f.write(res)
    f.close()
    
def batchRun(nprocess = 3):
    jars = os.listdir(JAR_DIR)
    pool = multiprocessing.Pool(processes = nprocess)
    inputs = os.listdir(TEST_DIR)
    for inp in inputs:
        for each in jars:
            if each != "specs-homework-3-1.3-raw-jar-with-dependencies.jar" and each[0] != '.':
                pool.apply_async(run, (each, inp))
    pool.close()
    pool.join()

      2 计时服务：提供时间统计服务，作为算法执行效率的参考。

      3 邮件通知：运行大规模测试很耗时，所以我是在树莓派上跑的，隔一段时间check一下树莓派很麻烦，所以我设置邮件通知方法，运行完以后向我发送邮件。

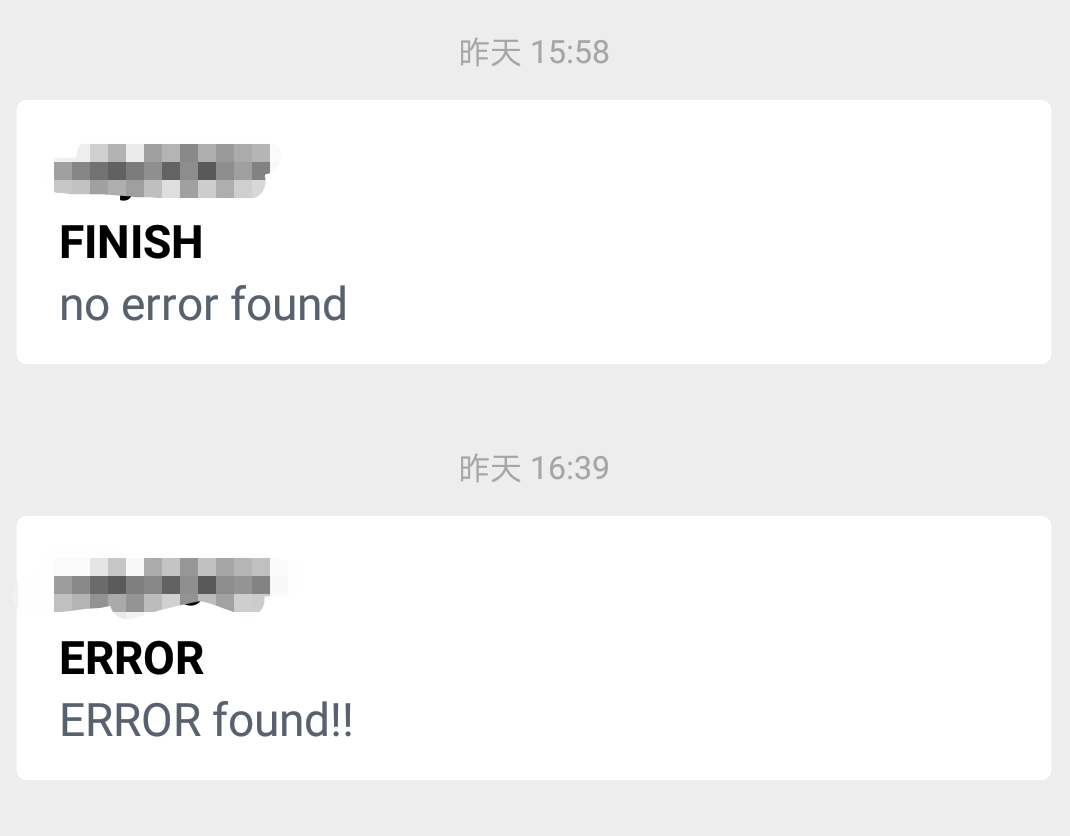
      当没有发现不同时，部分结果如下：

 

      具体技术细节见开源代码库：https://github.com/sdycodes/JavaDestroyCorner.git  (开源已经过jar包拥有者同意)

六、心得体会

      JML最大的特点是规范与灵活的综合。

      从规范的方面来看，因为有了规格对方法实现目标的描述，所以其实并不需要对全局有什么认识就可以完成代码。在实现这些方法的时候感觉自己像流水线上的工人。

      从灵活的方面来看，仅仅依靠规格把方法实现是不够的。这样最多也只能保证正确性，但是确不能保证效率，第一次作业中只是按照规格写完了代码，但是没有考虑时间复杂度的问题，导致最后四个点惨遭TLE，这也说明了满足规格是实现方法的必须要求，但并不是方法实现的全部要求。JML规定了需要满足的条件，除此之外的部分则是各显神通的自由空间。