这题是寒假快要结束的时候做的(已经开学一周啦),因为自己写的代码有超时,百度后看了康托展开,然后优化成功,花了比较长的时间。题目如下:
问题描述
如下面第一个图的九宫格中,放着 1~8 的数字卡片,还有一个格子空着。与空格子相邻的格子中的卡片可以移动到空格中。经过若干次移动,可以形成第二个图所示的局面。
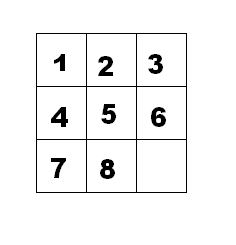
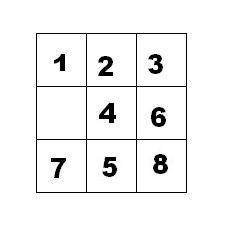
我们把第一个图的局面记为:12345678.
把第二个图的局面记为:123.46758
显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
本题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出-1。
我们把第一个图的局面记为:12345678.
把第二个图的局面记为:123.46758
显然是按从上到下,从左到右的顺序记录数字,空格记为句点。
本题目的任务是已知九宫的初态和终态,求最少经过多少步的移动可以到达。如果无论多少步都无法到达,则输出-1。
输入格式
输入第一行包含九宫的初态,第二行包含九宫的终态。
输出格式
输出最少的步数,如果不存在方案,则输出-1。
样例输入
12345678.
123.46758
123.46758
样例输出
3
样例输入
13524678.
46758123.
46758123.
样例输出
22
---------分割线---------
此题因为是找最短路径,所以用bfs,不懂康拓展开的可以百度一下,我的代码用到的康拓展开就是把所有的排列情况做了一个折叠,折叠成了一个数,例如.12345678折叠成了0,87654321.折叠成了9!-1(总的排列情况有9!种),这样就可以开一个40万的数组记录当前情况是否已经出现过,即判重,用康拓展开后,我的程序就通过测评了,具体见代码吧。
1 #include<stdio.h> 2 typedef struct Point 3 { 4 int now[9]; 5 int x; 6 int step; 7 }point; 8 point init,goal; 9 point T[400000]; 10 int vis[400000]; 11 int E[9]={1,1,2,6,24,120,720,5040,40320}; 12 int move[4][2] ={-1,0,1,0,0,-1,0,1}; 13 int start=0,end=0; 14 void add(point p)//此函数和下一个函数都是队列操作 15 { 16 T[end]=p; 17 end++; 18 } 19 void del() 20 { 21 start++; 22 } 23 int cantor(int *A)//康拓展开 24 { 25 int i,j,s=0,n; 26 for(i=0;i<9;i++) 27 { 28 n=0; 29 for(j=i+1;j<9;j++) 30 if(A[i]>A[j]) 31 n++; 32 s+=n*E[8-i]; 33 } 34 return s; 35 } 36 void bfs() 37 { 38 int t,g=cantor(goal.now); 39 point p; 40 p=init; 41 add(p); 42 vis[cantor(init.now)]=1; 43 while(end-start>0) 44 { 45 p=T[start]; 46 if(cantor(p.now)==g) 47 { 48 printf("%d",p.step); 49 return; 50 } 51 int i,x,y,x0,y0; 52 x=p.x/3,y=p.x%3; 53 for(i=0;i<4;i++) 54 { 55 x0=x+move[i][0]; 56 y0=y+move[i][1]; 57 if (x0<0||x0>2||y0<0||y0>2) 58 continue; 59 point q=p; 60 q.x=x0*3+y0; 61 q.step++; 62 q.now[p.x]=q.now[q.x]; 63 q.now[q.x]=0; 64 t=cantor(q.now); 65 if(!vis[t]) 66 { 67 vis[t]=1; 68 add(q); 69 } 70 } 71 del(); 72 } 73 printf("-1"); 74 } 75 int main() 76 { 77 int i; 78 char a[10],b[10]; 79 scanf("%s%s",a,b); 80 for(i=0;i<9;i++) 81 { 82 if(a[i]!='.') 83 init.now[i]=a[i]-'0'; 84 else 85 { 86 init.now[i]=0; 87 init.x=i; 88 } 89 if(b[i]!='.') 90 goal.now[i]=b[i]-'0'; 91 else 92 goal.now[i]=0; 93 } 94 init.step=0; 95 bfs(); 96 return 0; 97 }