冒泡排序

一种简单的排序算法；重复的走访整个序列，一次比较相邻的两个元素，如果顺序不一致就将它们交换过来；走访序列的工作是重复进行的，直到没有再需要交换的元素，即表示这个序列已排序完成；这个算法的名字由来是因为越小（或越大）的元素会经由交换慢慢"浮"到序列的一端

   

假设有一个无序序列 L0、L1、L2、…、Ln-1

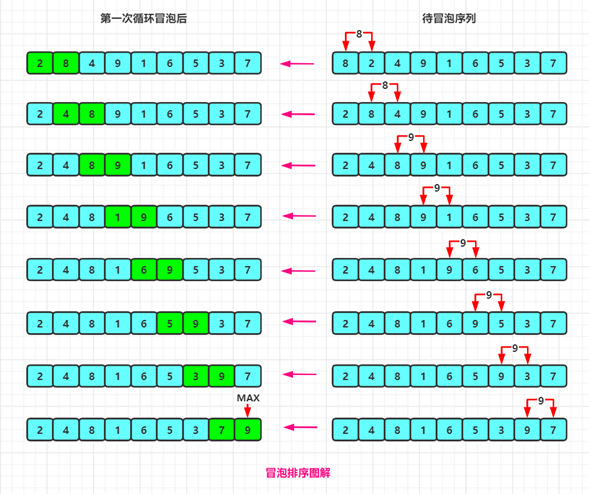
• 比较相邻两个元素 Li、Li-1 ，按照一定的规则（降序或升序）比较，进行交换
• 对每一对相邻元素做同样的比较交换，从开始的第一对 L0 ~ L1 到结尾最后的一对 Ln-2 ~ Ln-1 ，这样在最会的元素要么是最大的要么是最小的
• 针对所有的元素重复以上的步骤，每进行一次循环后，必然会取出一个极值
• 重复步骤 1~3，直到排序完成

　　　　　　

import java.util.Arrays;

/**
 * 方案1
 * @date 2020/8/20 11:04
 */
public class TestSort {

    public static void main(String[] args) {
               // 待排序数组 
        int[] arr = {8, 2, 4, 12, 4, 10, 3, 11, 1};
        System.out.println(Arrays.toString(arr));
               // 排好序数组
        int[] sort = bubbleSort(arr);
        System.out.println(Arrays.toString(sort));
    }

       // 常规版本
    private static int[] bubbleSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            for (int j = 0; j < arr.length - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
        return arr;
    }
}

import java.util.Arrays;

/**
 * 方案2
 */
public class TestSort {

    public static void main(String[] args) {
        int[] arr = {8, 2, 4, 12, 4, 10, 3, 11, 1};
        System.out.println(Arrays.toString(arr));
        int[] sort = bubbleSort(arr);
        System.out.println(Arrays.toString(sort));
    }

       // 升级版本1
    private static int[] bubbleSort(int[] arr) {
        for (int i = 1; i < arr.length; i++) {
            // 标志是否有交换
            boolean flag = false;
            for (int j = 0; j < arr.length - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    flag = true;
                }
            }
            // 无交换表明序列已然有序
            if (!flag) {
                break;
            }
        }
        return arr;
    }
}

　　

import java.util.Arrays;

/**
 * 方案3
 * @date 2020/8/20 11:04
 */
public class TestSort {

    public static void main(String[] args) {
        int[] arr = {8, 2, 4, 12, 4, 10, 3, 11, 1};
        System.out.println(Arrays.toString(arr));
        int[] sort = bubbleSort(arr);
        System.out.println(Arrays.toString(sort));
    }

       // 升级版本2
    private static int[] bubbleSort(int[] arr) {
        int len = arr.length - 1;
        // 记录最后一次交换的位置
        int tempPosition = 0;
        for (int i = 1; i < arr.length; i++) {
            // 标志是否有交换
            boolean flag = false;
            for (int j = 0; j < len; j++) {
                if (arr[j] > arr[j + 1]) {
                    int temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                    // 发生交换，标志 true
                    flag = true;
                    // 记录交换的位置
                    tempPosition = j;
                }
            }
            // 把最后一次交换的位置给 len，来缩减内循环的次数
            len = tempPosition;
            // 无交换表明序列已然有序
            if (!flag) {
                break;
            }
        }
        return arr;
    }
}