2298. 异或
(File IO): input:gcdxor.in output:gcdxor.out
时间限制: 1000 ms 空间限制: 262144 KB 具体限制
题目描述
SarvaTathagata是个神仙,一天他在研究数论时,书上有这么一个问题:求不超过n两两的数的gcd。
SarvaTathagata这么神仙的人当然觉得这个是sb题啦。学习之余,他还发现gcd的某一个特别好的性质:如果有两个数i,j满足gcd(i,j)=i^j(这里的^为c++中的异或)的话,那么这两个数组成的数对(i,j)就是一个nb的数对(这里认为(i,j)和(j,i)为相同的,并不需要计算2次)。
当然,SarvaTathagata并不会只满足于判断一个数对是否nb,他还想知道满足两个数都是不超过n并且nb的数对有多少个。
由于SarvaTathagata实在是太神仙了,他认为这种题实在是太简单了。于是他找到了你,看看你是否能解决这个问题。
输入
共一行一个整数n,含义如题所述。
输出
一行一个整数,表示nb的数对的个数。
样例输入
样例输入1
12
样例输入2
123456
样例输出
样例输出1
8
样例输出2
214394
数据范围限制
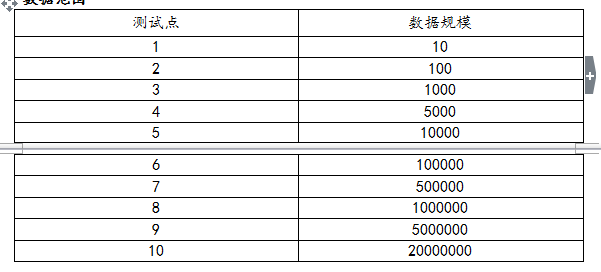
提示
样例1中共有八对,分别是: {1,3},{1,5},{1,7},{1,9},{2,6},{1,11},{2,10},{4,12}。
提示有误,特此隐藏
Solution
这是一道数论题,涉及gcd,xor(^),二进制减法。
以上三者中,若你对任何一样过敏,请谨慎食用。
Way one(40分)
用个程序找规律

//gcdxor table #include<bits/stdc++.h> using namespace std; int gcd(int ta,int tb) { if(tb==0) return ta; if(ta%2!=0&&tb%2!=0) return gcd(tb,ta%tb); if(ta%2==0&&tb%2!=0) return gcd(ta/2,tb); if(ta%2!=0&&tb%2==0) return gcd(ta,tb/2); return 2*gcd(ta/2,tb/2); } int ans[10000001]; int n; bool vis[10000001],memory[1001][1001];//memory[i][j] int search(int num) { if(vis[num]) return ans[num]; if(num==1) return 0; vis[num]=1; int now=0; for(int i=1;i<num;i++) { if(gcd(num,i)==(num xor i)) now++; // if(gcd(i,num)==(i xor num)) // now++; } // if(gcd(num,num)==(num xor num)) // now++; ans[num]=ans[num-1]+now; return ans[num]; } int main() { freopen("table4.txt","w",stdout); cin>>n; // int s=clock(); int k; /* for(k=0;k<=n;k++) { if(k==0) {cout<<0<<endl;continue;} for(int i=1;i<=k;i++) { for(int j=1;j<=k;j++) { if(gcd(i,j)==(i xor j)){ memory[i][j]=true; ans[k]++; } // cout<<memory[i][j]<<" "; } // cout<<endl; } cout<<k<<" "<<ans[k]/2<<endl; } */ // /* for(int k=0;k<=n;k++) { if(k==0) {cout<<0<<endl;continue;} cout<<k<<" "<<search(k)<<","<<endl; } // */ // int e=clock(); // cout<<e-s; return 0; }
找不到……
Code(40分)

#pragma GCC optimize(2) #include<bits/stdc++.h> #define IL inline using namespace std; short int diff[2001]{0,0,0,1,0,1,1,1,0,1,1,1,1,1,1,3,0,1,1,1,1,1,1,1,1,1,1,3,1,1,3,1,0,1,1,1,1,1,1,2,1,1,1,1,1,3,1,1,1,1,1,3,1,1,3,2,1,1,1,1,3,1,1,5,0,1,1,1,1,1,1,1,1,1,1,2,1,1,2,1,1,1,1,1,1,3,1,2,1,1,3,1,1,1,1,3,1,1,1,3,1,1,3,1,1,1,1,1,3,1,2,3,1,1,1,1,1,1,1,3,3,1,1,3,1,3,5,1,0,1,1,1,1,1,1,3,1,1,1,1,1,1,1,3,1,1,1,2,1,1,2,1,1,3,1,1,2,1,1,2,1,1,1,1,1,3,1,1,1,1,3,3,1,1,2,4,1,1,1,1,3,1,1,2,1,1,1,3,1,3,3,1,1,1,1,3,1,1,3,1,1,1,1,1,3,2,1,4,1,1,1,1,1,1,1,2,3,1,1,3,2,3,3,1,1,1,1,1,1,1,1,4,1,1,1,1,1,1,3,1,3,1,1,3,1,3,3,2,1,1,3,1,5,1,1,7,0,1,1,1,1,1,1,1,1,1,1,2,1,1,3,1,1,1,1,1,1,1,1,2,1,1,1,1,1,2,3,2,1,1,1,2,1,1,2,2,1,3,1,1,2,1,1,2,1,1,3,1,1,1,1,1,2,1,1,4,1,1,2,3,1,1,1,1,1,3,1,2,1,1,3,1,1,2,1,3,1,1,1,2,3,1,3,2,1,1,1,1,2,1,4,5,1,1,1,1,1,1,1,1,3,1,1,4,1,3,2,1,1,1,1,1,1,1,3,3,1,1,3,1,3,1,1,1,1,1,1,3,1,1,3,1,1,1,1,1,3,1,1,4,1,1,1,1,1,2,1,1,3,1,2,3,1,1,4,2,1,1,1,1,1,1,1,2,1,1,1,1,1,3,2,1,3,1,1,3,1,1,3,1,2,3,3,1,3,2,1,3,1,1,1,1,1,1,1,4,1,1,1,3,1,1,4,1,1,1,1,1,1,1,1,2,1,1,1,3,3,2,1,1,3,1,1,3,1,3,3,1,1,1,3,1,3,1,2,10,1,1,1,1,3,1,1,1,5,1,1,3,1,1,7,3,0,1,1,1,1,1,1,2,1,1,1,1,1,2,1,1,1,1,1,2,1,1,2,2,1,1,1,2,3,1,1,2,1,1,1,1,1,1,1,1,1,1,1,2,1,1,2,3,1,3,1,1,1,2,1,4,1,1,2,1,3,1,2,4,1,1,1,2,1,1,2,1,1,3,1,1,2,1,2,2,1,1,3,2,1,1,1,1,2,1,1,4,1,2,2,1,1,1,1,1,3,1,1,3,1,1,1,1,1,3,1,2,2,1,1,4,1,3,4,1,1,1,1,1,2,3,3,4,1,1,1,1,1,3,1,1,1,1,3,2,1,1,2,3,1,1,1,1,3,1,1,3,1,1,2,1,1,1,3,2,1,1,1,2,1,1,2,2,3,1,1,1,3,3,2,2,1,1,1,1,1,3,1,2,2,3,1,2,4,1,5,3,1,1,1,1,1,1,1,2,1,1,1,3,1,1,1,1,3,1,1,2,1,3,4,1,1,3,3,2,2,1,1,7,1,1,1,1,1,1,1,1,1,1,1,3,3,1,3,1,1,1,1,1,3,1,1,5,3,1,1,1,1,7,1,3,1,1,1,3,1,1,3,2,1,1,1,1,3,1,1,4,1,1,1,1,1,1,1,2,3,1,1,3,1,1,4,2,1,1,1,1,1,2,1,2,1,1,2,1,1,1,1,2,3,1,1,3,2,1,3,1,1,3,1,1,4,1,2,3,1,1,1,1,1,1,1,1,1,1,1,2,1,4,2,4,1,1,1,1,1,1,1,4,1,1,3,1,2,2,1,1,3,1,1,3,1,1,3,2,1,3,1,2,3,1,1,3,2,1,3,1,3,2,1,1,3,1,2,9,1,1,3,2,1,1,1,1,1,1,1,4,1,1,1,1,1,2,4,1,1,1,1,2,1,1,3,1,1,1,1,1,4,3,1,3,1,1,1,1,1,1,1,2,1,1,1,2,1,1,2,2,1,1,1,1,1,1,3,2,3,1,2,1,1,3,1,3,3,1,1,3,1,3,3,1,1,1,3,1,3,1,1,9,1,1,1,1,3,1,1,1,3,1,1,3,2,1,10,1,1,1,1,1,1,1,1,3,3,1,1,1,1,3,1,1,5,1,1,3,1,1,3,5,1,3,1,1,7,1,3,7,0,1,1,1,1,1,1,1,1,1,1,3,1,1,2,1,1,1,1,1,1,2,1,2,1,1,2,1,1,3,1,2,1,1,1,2,1,1,2,1,1,1,1,2,2,1,2,4,1,1,1,1,1,1,2,1,3,1,1,4,1,2,2,1,1,1,1,1,1,1,1,3,1,1,1,1,1,1,1,1,1,3,1,2,1,1,2,1,1,1,1,1,2,1,3,2,1,1,3,1,1,2,1,2,1,1,2,2,1,1,4,2,1,1,1,3,2,1,1,2,3,1,1,1,2,1,4,1,1,1,1,2,1,1,2,1,1,3,1,1,2,2,1,2,1,1,3,1,1,2,1,2,2,1,1,4,2,1,2,3,1,1,1,1,3,1,2,2,1,1,1,1,1,3,1,2,2,1,1,2,1,2,4,2,1,1,2,1,2,1,1,8,1,1,1,1,1,1,1,1,3,1,1,2,1,1,3,1,1,1,1,3,1,1,1,4,1,3,3,2,1,2,2,2,2,1,1,2,1,1,4,2,1,1,3,1,4,3,1,2,1,1,1,1,1,1,1,1,2,1,3,6,3,1,4,1,1,1,1,1,1,3,1,2,1,1,3,1,1,1,1,4,1,1,1,2,3,1,2,1,1,2,1,1,2,2,3,4,1,1,1,1,1,1,1,1,3,1,1,3,1,3,3,1,1,1,1,1,2,1,1,3,1,1,1,1,3,2,2,2,1,1,1,2,1,1,2,2,1,1,1,1,2,1,2,3,3,1,1,1,1,5,1,1,3,1,3,2,2,1,2,5,1,1,1,1,1,1,1,2,1,1,3,2,1,1,2,3,2,1,3,2,1,1,2,1,4,1,1,1,5,3,3,5,1,1,1,1,1,1,1,2,1,1,1,4,1,1,2,1,1,1,1,1,1,1,3,2,1,1,1,1,1,1,1,1,3,1,1,2,1,3,2,1,1,3,3,1,4,1,1,5,1,1,3,1,3,1,2,4,2,1,1,4,1,2,7,1,1,1,1,1,1,1,1,2,1,1,1,1,1,3,1,1,1,1,1,2,1,1,3,4,3,1,1,1,3,1,1,3,1,1,1,1,1,1,1,1,3,1,1,2,1,3,5,2,3,1,1,1,1,3,1,2,1,1,7,1,1,3,3,3,1,1,1,3,1,1,3,1,1,1,1,1,3,1,2,4,1,1,1,1,1,1,1,1,3,1,1,3,1,2,4,1,1,1,1,1,1,1,1,5,1,1,1,1,1,1,2,1,3,1,1,3,1,1,3,2,1,2,1,2,4,1,2,6,1,1,1,1,1,2,1,1,1,1,2,3,1,1,2,2,1,1,1,1,2,1,1,2,1,3,1,1,1,2,2,2,3,1,1,3,1,1,3,1,2,1,1,1,3,2,1,4,1,3,3,1,1,1,1,2,4,1,1,3,2,1,3,1,1,1,1,1,1,1,1,2,1,1,1,1,1,3,1,1,1,1,1,3,1,2,2,2,1,1,4,2,2,1,4,4,1,1,1,1,1,1,1,2,1,1,1,2,1,1,4,1,1,1,1,3,3,2,1,2,2,1,2,1,1,3,1,3,3,1,1,3,1,1,3,2,1,3,1,1,3,1,2,4,1,1,3,1,1,1,2,2,3,1,1,7,1,1,3,1,2,1,1,1,3,2,1,2,3,1,2,3,1,3,1,3,3,1,1,3,2,1,9,1,1,3,1,1,3,1,2,5,1,1,1,1,1,1,1,3,1,1,1,2,1,2,4,2,1,1,1,1,1,1,1,3,1,1,2,2,4,1,1,1,1,1,1,2,1,1,2,1,1,1,1,1,3,1,1,2,1,1,1,2,1,2,1,1,4,1,3,2,1,2,3,6,1,1,1,1,1,1,1,3,1,1,1,1,1,1,2,1,1,1,1,2,1,1,2,1,1,2,1,1,2,5,2,3,1,1,1,1,1,1,1,2,1,1,1,3,3,1,2,2,3,1,1,1,2,1,1,7,1,1,3,1,1,2,3,3,3,1,1,3,1,3,3,1,1,1,3,1,3,1,1,8,1,1,1,1,3,1,1,1,3,1,1,4,1,1,9,1,1,1,1,1,1,1,1,2,3,1,1,1,1,3,1,2,3,1,1,3,1,1,3,2,2,1,1,1,10,1,1,3,1,1,1,1,1,1,1,1,1,1,1,2,1,1,3,1,3}; int n,ans; IL int gcd(int ta,int tb) { if(tb==0) return ta; if(ta%2!=0&&tb%2!=0) return gcd(tb,ta%tb); if(ta%2==0&&tb%2!=0) return gcd(ta/2,tb); if(ta%2!=0&&tb%2==0) return gcd(ta,tb/2); return 2*gcd(ta/2,tb/2); } IL int search(int num) { if(num==2000) { int t=0; for(int i=0;i<=2000;i++) t+=diff[i]; return t; } int prev; if(num>2000) prev=search(num-1); int now=0; for(int i=1;i<num;i++) if(gcd(num,i)==(num xor i)) now++; if(gcd(num,num)==(num xor num)) now++; return prev+now; } int main() { freopen("gcdxor.in","r",stdin); freopen("gcdxor.out","w",stdout); cin>>n; for(int i=0;i<=min(n,2000);i++) ans+=diff[i]; if(n<=2000) cout<<ans<<endl; else cout<<search(n)<<endl; return 0; }
其实,要是我愿意我可以把表全打出来,但是这个OJ有代码长度限制(5kb)。有毒……
Way two
从大神视角理解这道题:
看到gcd就去想数论嘛
求证:若gcd(a,b)=a xor b,则gcd(a,b)=a-b (a≥b)
转到完整证明
证明:
由更相减损法,可知gcd(a,b)=gcd(b,a-b)
这个的原理与辗转相除法类似,只是把求模换成了减法
若a-b=0,则gcd(a,b)=gcd(b,a-b)=a=b
否则a-b>0,此时gcd(a,b)=gcd(b,a-b)>a-b
所以,gcd(a,b)≥a-b
再分析xor运算和二进制减法
xor:对与每一位,若是相同则为0,若是不同则得1
1^1=0 1^0=1 0^1=1 0^0=0
减法:对于每一位,若是相同则得0,若是1 0则得1,若是0 1则得1并使上一位-1
1-1=0 1-0=1 0-1=-1 0-0=0

那么,如果两数a,b中出现了0->1的情况,则减法会使那一位上出现退位,异或(xor)则不会
所以,a xor b≥a-b
又因为(前面证明的)gcd(a,b)≥a-b
所以gcd(a,b)≥a-b≥a xor b
所以当gcd(a,b)=a xor b时,gcd(a,b)=a-b=a xor b
所以若gcd(a,b)=a xor b,则gcd(a,b)=a-b (a≥b)
证毕
回到此题
现在我已经证出来
若gcd(a,b)=a xor b,则gcd(a,b)=a-b (a≥b)
一看题目,就是当gcd(a,b)=a xor b时
那么我们就可以直接用结论了
设c=a-b,则b=a-c
若数对(a,b)符合条件
则c=a^b
故我只要枚举a和b即可!
Code(90分)
#pragma GCC optimize(2)//这个程序不开O2会超时(90分) #include<bits/stdc++.h> using namespace std; int n,cnt[20000001],sum[20000001]; int main() { // freopen("gcdxor.in","r",stdin); // freopen("gcdxor.out","w",stdout); cin>>n; memset(cnt, 0, sizeof(cnt)); for(int c = 1; c <= n; c++) for(int a = c*2; a <= n; a += c) //因为a>=b,所以需要从2*c开始枚举 { int b = a - c; if(c == (a ^ b)) cnt[a]++;//统计每个a对应的b的数量 }//^的优先级低于==,所以要打上括号 sum[0] = 0; for(int i = 1; i <= n; i++) sum[i] = sum[i-1] + cnt[i]; cout<<sum[n]; return 0; }
Code(100分)
#include<bits/stdc++.h> using namespace std; int n,sum; int main() { // freopen("gcdxor.in","r",stdin); // freopen("gcdxor.out","w",stdout); scanf("%d",&n); // int s=clock(); for(int c=1;c<=n;c++)//c=a-b for(int a=c*2;a<=n;a+=c) //因为a>=b,所以需要从2*c开始枚举 if(c==(a ^ (a-c))) sum++; //统计每个a对应的b的数量 //^的优先级低于==,所以要打上括号 printf("%d",sum); // int e=clock(); // cout<<endl<<e-s; return 0; }
TLE?
细心的你应该发现这个:

不要怕TLE啦
如果你会算复杂度,会一点微积分,会一点金融学,你就要知道:
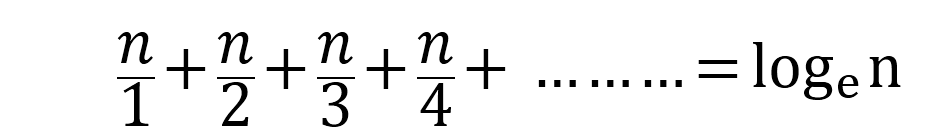
所以整个程序的时间复杂度为O(nlog(n))
Attention
一、^的优先级低于==,所以要打上括号
二、因为a>=b,所以需要从2*c开始枚举,使得a的最小值为2*c,b=a-c,b的初值值为c且越来越小
三、用前缀和的思想,递归sum[i] = sum[i-1] + cnt[i],即n的答案是在n-1的基础上加上这次枚举的答案
END
