迪杰斯特拉算法-文档读取数据

迪杰斯特拉算法总结：
读取文档readTxtFile(filePath);
生成二维数组createArray（filePath）；（注意每行的第一个数字顶头写，否则会读入空格）
二维数组String型转int型str2int（String[][] str）；
迪杰斯特拉：
起始点vs到其他节点的最短路径；
过程：
1.顶点分两组：S(已经求出最短路径的顶点),U=V-S（剩余的顶点），初始状态S只包含vs；
2.从U中选择一个距离vs最近的顶点vnear加入S；
3.更新U的后继顶点的最短路径长度；
4.重复2，3直到U=NULL；
算法实现：
定义前驱顶点数组prenode[]，即prenode[i]的值是顶点vs到顶点vf的最短路径所经历的全部顶点
中，位于顶点vf之前的那个顶点；
定义path[]，储存vs到vf最短路径的长度；
初始化://每个顶点到vs的最短路径就是两个顶点之间的权值

for (int i = 0; i <path.length; i++) {
            prenode[i] = i;
            path[i] = Graph[vs][i];//顶点i的最短路径为顶点vs到i的权
            flag[i] = false;
        }
flag[vs] = true;//vs自身初始化

遍历 Graph.length-1次，找出每个顶点的最短路径：

寻找最短vnear以及权值，

// 每次循环求得当前距离vs最近的顶点vnear和最短距离min
            int min = 100000;//100000表示无穷
            for (int j = 0; j < Graph.length; j++) {
                if (!flag[j] && path[j] < min) {
                    min = path[j];
                    vnear = j;
                }
            }

更新数据

// 根据vnear更新vs到其他所有节点的前驱节点和最短路径
            for (int k = 0; k < Graph.length; k++) {
                if (!flag[k] && (min + Graph[vnear][k]) < path[k]) {
                    prenode[k] = vnear;
                    path[k] = min + Graph[vnear][k];
                }
            }

求得最短路径输出

源代码：

import java.io.BufferedReader;
import java.io.File;
import java.io.FileInputStream;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;

public class Dijkstra{
    public static void main(String[] args) throws IOException{
         @SuppressWarnings("resource")
        Scanner sc=new Scanner(System.in);
         System.out.println("输入起点与终点:");
         int a[]=new int[2];
         for(int i=0;i<2;i++){
                a[i]=sc.nextInt();
         }
         int vs=a[0];
         int vf=a[1];
         Dijkstra.dijkstra(vs,vf);
    }
    public static  List<String>  readTxtFile(String filePath) {
        /**
         * 读取文档
         * @param filePath
         * @return
         */
                List<String> list = new ArrayList<String>();
                try {
                    String encoding = "UTF-8";
                    File file = new File(filePath);
                    if (file.isFile() && file.exists()) { 
                        InputStreamReader read = new InputStreamReader(
                                new FileInputStream(file), encoding);
                        BufferedReader bufferedReader = new BufferedReader(read);
                        String lineTxt = null;
                        while ((lineTxt = bufferedReader.readLine()) != null) {
                            if (!lineTxt.startsWith("#"))
                                list.add(lineTxt);
                        }
                        read.close();
                    } else {
                        System.out.println("找不到文件");
                    }
                } catch (Exception e) {
                    System.out.println("出错了");
                    e.printStackTrace();
                }
                return list;
          
            }
    
    
    public static String[][] createArray(String filePath){
        /**
         * 读取文档生成二维数组
         * @param filePath
         * @return
         */
            List<String> list = readTxtFile(filePath);
            System.out.println("读取成功");
            String[][] array = new String[list.size()][];
            for(int i=0;i<list.size();i++){
                array[i] = new String[list.size()];
                String linetxt=list.get(i);
                String[] myArray = linetxt.replaceAll("\s+", "@").split("@");
                for(int j=0;j<myArray.length;j++){
                        array[i][j]=myArray[j];                                        
                }
            }
            return array;
        }
    
    public static int[][] str2int(String[][] str)
    {
        int a,b;
        a = str.length;
        b = str[0].length;
        int result[][] = new int[a][b];
        for(int i = 0 ; i < a ; ++ i)
            for(int j = 0 ; j < b ; ++ j) {
                result[i][j] = Integer.parseInt(str[i][j]);
            }
                
        return result;
    }
    public static void printArray(String array[][]){//打印输出，观察二维数组是否正确；纠错用
        for(int i=0;i<array.length;i++){
            for(int j=0;j<array[i].length;j++){
                if(j!=array[i].length-1){
                    System.out.print("array["+i+"]["+j+"]="+array[i][j]+",");
                }
                else{
                    System.out.print("array["+i+"]["+j+"]="+array[i][j]);
                }
                  
            }
            System.out.println();
        }
    }
    public static void dijkstra(int vs,int vf) {
        /**
        * Dijkstra最短路径。
        * 即图中"节点vs"到其它各个节点的最短路径。
        * @param vs 起始节点
        * @param Graph 图
         */
        int array[]= {-1,-1,-1,-1,-1,-1,-1,-1,-1,-1};//将最短路径上的顶点，距离存入数组，返回
        String[][] str= createArray("D:\text.txt");
        System.out.println("成功创建二维字符串数组");
         printArray(str);
        //将读取的String型二维数组转化为int型       
        int[][]Graph =str2int(str);    
        System.out.println("成功转化为整数组");
        int NUM = Graph[0].length;
        
        
        int[] prenode = new int[NUM];// 前驱节点数组
        
        
        int[] path = new int[NUM];// 最短距离数组
        
        
        boolean[] flag = new boolean[NUM];// 该节点是否已经找到最短路径
         
        int vnear = 0;//距离vs最近的节点
        
        //初始化
        for (int i = 0; i <path.length; i++) {
            prenode[i] = i;
            path[i] = Graph[vs][i];//顶点i的最短路径为顶点vs到i的权
            flag[i] = false;
        }
 
        flag[vs] = true;//vs自身初始化
        
        //遍历 Graph.length-1次，找出每个顶点的最短路径
        for (int v = 1; v < Graph.length; v++) {
            // 每次循环求得当前距离vs最近的顶点vnear和最短距离min
            int min = 100000;//100000表示无穷
            for (int j = 0; j < Graph.length; j++) {
                if (!flag[j] && path[j] < min) {
                    min = path[j];
                    vnear = j;
                }
            }
            //标记顶点vnear为已经获取到最短路径
            flag[vnear] = true;
            
            // 根据vnear更新vs到其他所有节点的前驱节点和最短路径
            for (int k = 0; k < Graph.length; k++) {
                if (!flag[k] && (min + Graph[vnear][k]) < path[k]) {
                    prenode[k] = vnear;
                    path[k] = min + Graph[vnear][k];
                }
            }
        }
        System.out.println("总公里数=" + path[vf]);
        System.out.println("起点"+vs+"到终点"+vf+"的最短路径为：");
        System.out.print("终点" + vf +"<-" + "前驱" + prenode[vf]);
        //依次输出前驱
        do{
            vf=prenode[vf];
            System.out.print("<-前驱" + prenode[vf]);
        }while(prenode[vf]==vs);
        System.out.println("<-起点" +vs);
        
    }  
}

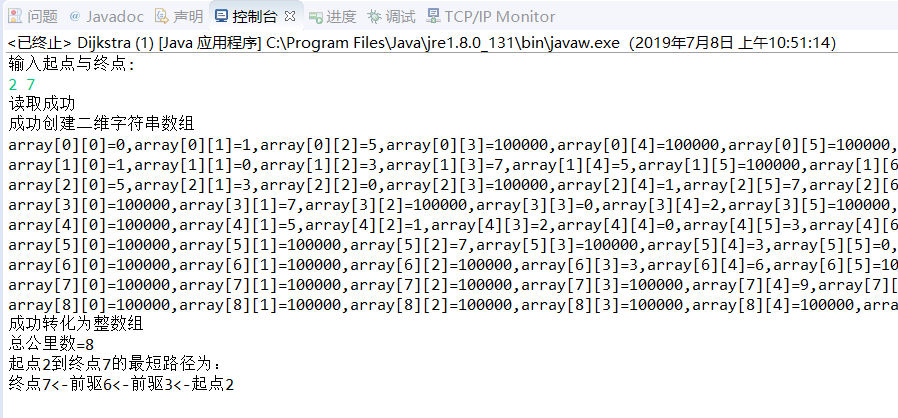
运行截图：