Logistic Regression Using Gradient Descent -- Binary Classification 代码实现

1. 原理

Cost function

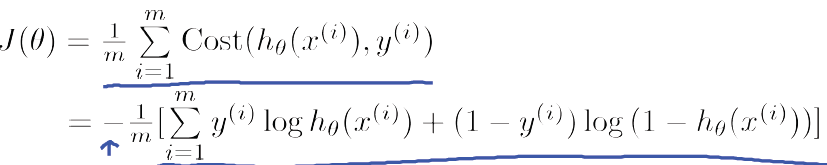
Theta

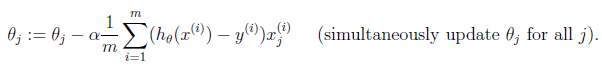
2. Python

# -*- coding:utf8 -*-
import numpy as np
import matplotlib.pyplot as plt


def cost_function(input_X, _y, theta):
    """
    cost function of binary classification using logistic regression
    :param input_X: np.matrix input X
    :param _y: np.matrix y
    :param theta: np.matrix theta
    """
    m = input_X.shape[0]
    z = input_X * theta
    h = np.asmatrix(1 / np.asarray(1 + np.exp(-z)))
    J = 1.0 / m * (np.log(h) * _y.T + np.log(1 - h) * (1 - _y).T)
    return J


def gradient_descent(input_X, _y, theta, learning_rate=0.1,
                     iterate_times=3000):
    """
    gradient descent of logistic regression
    :param input_X: np.matrix input X
    :param _y: np.matrix y
    :param theta: np.matrix theta
    :param learning_rate: float learning rate
    :param iterate_times: int max iteration times
    :return: tuple
    """
    m = input_X.shape[0]
    Js = []

    for i in range(iterate_times):
        z = input_X * theta
        h = np.asmatrix(1 / np.asarray(1 + np.exp(-z)))
        errors = h - _y
        delta = 1.0 / m * (errors.T * input_X).T
        theta -= learning_rate * delta
        Js.append(cost_function(input_X, _y, theta))

    return theta, Js

3. C++

#include <iostream>
#include <vector>
#include <Eigen/Dense>

using namespace std;
using namespace Eigen;


double cost_function(MatrixXd &input_X, MatrixXd &_y, MatrixXd &theta):
  double m = input_X.rows();
  ArrayXd _z = 0 - (input_X * theta).array();
  ArrayXd h = 1.0 / (1.0 + _z.exp());
  double J = h.log().matrix() * _y.transpose() + 
      (1 - h).log().matrix() * (1 - _y.array()).matrix().transpose();
  return J


class GradientDescent{
  public:
    GradientDescent(MatrixXd &x, MatrixXd &y, MatrixXd &t, double r, 
                    int i): input_X(x), _y(y), theta(t), learning_rate(r),
                    iterate_times(i) {}
    MatrixXd theta;
    vector<double> Js;
    void run();
  private:
    MatrixXd input_X;
    MatrixXd _y;
    double learning_rate;
    int iterate_times;
}

void GradientDescent::run() {
  double rows = input_X.rows();
  for(int i=0; i<iterate_times; ++i) {
    ArrayXd _z = 0 - (input_X * theta).array();
    ArrayXd h = 1.0 / (1.0 + _z.exp());
    MatrixXd errors = h.matrix() - y;
    MatrixXd delta = 1.0 / rows * (errors.transpose() * input_X).transpose();
    theta -= learning_rate * delta;
    double J = cost_function(input_X, _y, theta);
    Js.push_back(J);
  }
}