参数
2D矩阵的表示 matrix(a,b,c,d,e,f),其中6个参数在矩阵的分布:
—— ——
| a c e |
| b d f |
| 0 0 1 |
—— ——
在CSS3中矩阵的原始值是这样的:
transform: matrix(1,0,0,1,0,0);
任意点(x,y,1)经过matrix变化为(ax+cy+e,bx+dy+f,1)
矩阵平移
matrix(1,0,0,1,e,f)
e: 矩阵x坐标平移值,正向平移e
f: 矩阵y坐标平移值,正向平移f
css3中方向,单位为px
|
|
--------->x
|
↓y
结论:平移只有跟e和f有关系,跟其他a,b,c,d没有关系,e对应x轴的平移,f对应y轴的平移,往正方向平移多少单位就加上多少单位,反之则减去多少个单位。
矩阵缩放
matrix(a,0,0,d,0,0)
a: 矩阵宽度缩放a倍,默认为1不缩放
d: 矩阵高度缩放d倍,默认为1不缩放
结论:缩放只有跟a和d有关系,跟其他数值都无关,a对应x轴缩放,d对应y轴缩放,缩放多少倍就乘以多少
矩阵旋转
matrix(cosθ,sinθ,-sinθ,cosθ,0,0);
sinθ和cosθ最大值为1 最小值为-1,当a b c f四个参数符合公式的规律是则为旋转
往顺时针方向旋转45°
a = cos45° = 0.707
b = sin45° = 0.707
c = -sin45° = -0.707
d = con45° = 0.707
matrix(0.707,0.707,-0.707,0.707,0,0);
往顺时针方向旋转90°
a = cos90° = 0
b = sin90° = 1
c = -sin90° = -1
d = con90° = 0
matrix(0,1,-1,0,0,0);
往顺时针方向旋转180°
a = cos180° = -1
b = sin180° = 0
c = -sin180° = 0
d = con180° = -1
matrix(0,1,-1,0,0,0);
结论:得知旋转的度数,根据用sin cos算出相应的值填写
矩阵拉伸
matrix(1,tanθ,tanθ,1,0,0)
b:矩阵以X轴做偏移,偏移后X轴和右边的角度Y°,tanY° = b的值 (左边不变,右边向Y正方向偏远)
c:矩阵以Y轴做偏移,偏移后Y轴和左边的角度X°,tanX° = c的值 (底边不变,顶边向X正方向偏远)
matrix(1,2,0,1,0,0)
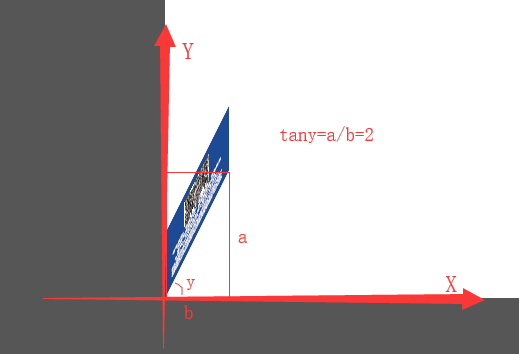
matrix(1,0,2,1,0,0)

参考
详细及原理请参考文章:
对CSS3中的transform:Matrix()矩阵的一些理解
https://www.cnblogs.com/Ivy-s/p/6786622.html
理解CSS3 transform中的Matrix(矩阵)
https://www.zhangxinxu.com/wordpress/2012/06/css3-transform-matrix-%E7%9F%A9%E9%98%B5/