一、向量积(外积、叉积)与数量积(内积、点积)
原理
叉积 http://baike.baidu.com/view/973423.htm
点积 http://baike.baidu.com/view/2744555.htm
两向量的叉乘(叉积、外积)仍然是一个向量:
- 这个向量的大小为原两向量模的乘积乘以其夹角的正弦值,也就是说在数值上等于两向量平移后形成的平行四边形的面积。
- 这个向量的方向是与两个原向量都垂直的方向,其指向用右手准则来判断。
参考自:https://www.zhihu.com/question/22902370
右手法则
叉乘右手法则:
当右手的四指从a以不超过180度的转角转向b时,竖起的大拇指指向是c的方向。
参考自:https://zhidao.baidu.com/question/98443003.html
返回值范围
点积(数量积)返回值范围:
两个普通向量点积返回值可以是无限大或无限小,两个单位向量点积返回值的范围大小:(-1, 1)。
以UE4数学函数为例,FVector::DotProduct(V1, V2) / (V1.Size() * V2.Size())等价于FVector::DotProduct(V1.GetSafeNormal(), V2.GetSafeNormal())。
差积(向量积)返回值范围:
向量积|c| = |a x b| = |a| |b| sin<a, b>
即c的长度在数值上等于以a,b,夹角为θ组成的平行四边形的面积。
而c的方向垂直于a与b所决定的平面,c的指向按右手定则从a转向b来确定。
向量叉乘与叉乘矩阵
向量叉乘与叉乘矩阵
https://www.cnblogs.com/monoSLAM/p/5349497.html
UE4中的点积、叉积函数
UE4的叉积(向量积、外积)函数:
FVector::CrossProduct()
UE4的点积(数量积、内积)函数:
FVector::DotProduct()
具体代码示例
FVector V1(100.f, 0.f, 0.f); FVector V2 = FRotator(0.f, 30.f, 0.f).RotateVector(V1); FVector V3 = FRotator(0.f, 45.f, 0.f).RotateVector(V1); FVector V4 = FRotator(0.f, 60.f, 0.f).RotateVector(V1); float d1 = FVector::DotProduct(V2, V3); float d2 = FVector::DotProduct(V3, V2); float d3 = FVector::DotProduct(V3, V4); float d4 = FVector::DotProduct(V2, V4);
其中各个值为:
V2 = (86.6f, 50.f, 0.f) V3 = (70.7f, 70.7f, 0.f) V4 = (50.f, 86.6f, 0.f) d1 = 9659.25781 d2 = 9659.25781 d3 = 9659.25781 d4 = 8660.25391
二、已知方向向量,求该向量与空间坐标轴的夹角
原始的数学公式不列举了,需要的话找个Math库看下源码。这里以UE4的API说明:
情况一:已知两个坐标点,求连线与空间坐标的夹角
已知空间中两个点FVector V1, V2,方向向量V3 = V2 - V1,求V3与空间坐标的夹角:
FRotator R = (V2 - V1).Rotation();
情况二:单个向量与世界坐标的夹角
已知方向向量Vector V1,求V1与空间坐标轴的夹角Rotator R1:即将Vector转换为Rotator
FRotator R1 = FVector(100.f, 100.f, 0.f).Rotation(); FRotator R2 = FVector(-100.f, -100.f, 0.f).Rotation(); FRotator R3 = FVector(100.f, 0.f, 0.f).Rotation(); FRotator R4 = FVector(0.f, 100.f, 0.f).Rotation();
结果分别是:
R1 = {Pitch=0.0 Yaw=45.0 Roll=0.0 }
R2 = {Pitch=0.0 Yaw=-135.0 Roll=0.0 }
R3 = {Pitch=0.0 Yaw=0.0 Roll=0.0 }
R4 = {Pitch=0.0 Yaw=90.0 Roll=0.0 }
FVector::Rotation()函数的内部实现(局部):
FRotator R; // Find yaw. R.Yaw = FMath::Atan2(Y,X) * (180.f / PI); // Find pitch. R.Pitch = FMath::Atan2(Z,FMath::Sqrt(X*X+Y*Y)) * (180.f / PI); // Find roll. R.Roll = 0; return R;
情况三:两个空间向量的夹角度数
FVector V1 = ...; FVector V2 = ...; float Angle = FMath::RadiansToDegrees(acosf(FVector::DotProduct(V1.GetSafeNormal(), V2.GetSafeNormal())));
运算结果值的范围为:0到180。
求点积时的两个向量一定要是单位向量,否则计算结果会大于Pi(正常范围是0到Pi)。
三、基于某点向某方向上投射指定距离后的坐标计算
代码:
float Len = FMath::Sqrt(100 * 100 + 100 * 100); FVector Loc = FVector(100.f, 100.f, 0.f) + FRotator(0.f, 45.f, 0.f).Vector() * Len;
结果:
Loc = {X=200.f, Y=200.f, Z=0.f}
FRotator::Vector()对应的蓝图函数为GetRotationXVector
=================================
例子2:
float Len = FMath::Sqrt(100 * 100 + 100 * 100); FVector Loc1 = FVector(0.f, 0.f, 0.f) + FRotator(0.f, 45.f, 0.f).Vector() * Len; FVector Loc2 = FVector(0.f, 0.f, 0.f) + FRotator(0.f, 135.f, 0.f).Vector() * Len; FVector Loc3 = FVector(0.f, 0.f, 0.f) + FRotator(0.f, 225.f, 0.f).Vector() * Len; FVector Loc4 = FVector(0.f, 0.f, 0.f) + FRotator(0.f, 315.f, 0.f).Vector() * Len;
结果:
Loc1 = {X=100.f, Y=100.f, Z=0.f}
Loc2 = {X=-100.f, Y=100.f, Z=0.f}
Loc3 = {X=-100.f, Y=-100.f, Z=0.f}
Loc4 = {X=100.f, Y=-100.f, Z=0.f}
四、如何检测某个点是否在多边形内部或者直线上
点在多边形内的判别方法
int pnpoly(int nvert, float *vertx, float *verty, float testx, float testy) { int i, j, c = 0; for (i = 0, j = nvert-1; i < nvert; j = i++) { if (((verty[i] > testy) != (verty[j] > testy)) && (testx < (vertx[j] - vertx[i]) * (testy - verty[i]) / (verty[j] - verty[i]) + vertx[i]) ) { c = !c; } } return c; }
Arguments
- nvert: Number of vertices in the polygon. Whether to repeat the first vertex at the end has been discussed in the article referred above.
- vertx, verty: Arrays containing the x- and y-coordinates of the polygon’s vertices.
- testx, testy: X- and y-coordinate of the test point.
https://stackoverflow.com/a/2922778/1645289
点在两点之间的直线上的判别方法
bool isLieOnLine() { dxc = currPoint.x - point1.x; dyc = currPoint.y - point1.y; dxl = point2.x - point1.x; dyl = point2.y - point1.y; //point lies on the line if and only if (dxc * dyl - dyc * dxl) is equal to zero. bool isCrossLine = dxc * dyl - dyc * dxl == 0; if(isCrossLine) { if (abs(dxl) >= abs(dyl)) return dxl > 0 ? point1.x <= currPoint.x && currPoint.x <= point2.x : point2.x <= currPoint.x && currPoint.x <= point1.x; else return dyl > 0 ? point1.y <= currPoint.y && currPoint.y <= point2.y : point2.y <= currPoint.y && currPoint.y <= point1.y; } return false; }
https://stackoverflow.com/a/11908158/1645289
参考
How to check if a given point lies inside or outside a polygon?
http://www.geeksforgeeks.org/how-to-check-if-a-given-point-lies-inside-a-polygon/
How to check if a point is inside a rectangle?
http://math.stackexchange.com/questions/190111/how-to-check-if-a-point-is-inside-a-rectangle
How can I determine whether a 2D Point is within a Polygon?
http://stackoverflow.com/questions/217578/how-can-i-determine-whether-a-2d-point-is-within-a-polygon#
How to check if a point lies on a line between 2 other points
https://stackoverflow.com/questions/11907947/how-to-check-if-a-point-lies-on-a-line-between-2-other-points
Check if a point belongs on a line segment
https://www.lucidar.me/en/mathematics/check-if-a-point-belongs-on-a-line-segment/
五、两个旋转矩阵(Rotation Matrix)相乘(Multiply)的几何意义
讲之前,先说下如果两个Rotation相加的意义,比如:
FRotator Rot1(0.f, 90.f, 0.f); FRotator Rot2(90.f,0.f, 0.f); FRotator Result = Rot1 + Rot2;
得到的结果FRotator Result(90.f, 90.f, 0.f),其意义是: 物体相对空间坐标原点的Rotation为(90.f, 90.f, 0.f),很好理解。
如果两个Rotation转换为Martix并相乘,比如:
FRotator Rot1(0.f, 90.f, 0.f); FRotator Rot2(90.f,0.f, 0.f); FRotator Result =( FRotationMatrix(Rot1) * FRotationMatrix(Rot2)).Rotator();
得到的结果FRotator Result(0.f, 90.f, 90.f),其意义是: 先将物体作Rot1旋转,即:Yaw方向(水平平面)旋转90度,然后再假设该物体相对坐标轴原点的旋转量为(0, 0, 0),即没有作任何旋转,但实际Rotation相对坐标轴原点为(0, 90, 0);然后再将物体进行Rot2旋转,即Pitch方向(垂直于(90, 0, 0)方向的平面)侧翻90度,因为侧翻90度前假设物体的Rotation是(0, 0, 0),所以侧翻时所在的平面不再是Yaw=90的平面(垂直于(0, 90, 0)方向),而是Yaw=0的平面(垂直于(90, 0, 0)方向)。没做相关配图,这段话理解起来有点绕,最好用空间思维想象下,可以用手掌比划。
实际应用:
比如空间中有两个物体:A和B,现在要将A旋转至与B相同的朝向,目前只知道A的相对世界坐标的Rotation Rw(90.f,0.f, 0.f)、B相对A(将A的Rotation当做(0, 0, 0))的Rotation Rr(0.f, 90.f, 0.f),求A旋转后的世界坐标Rotation。
此时的计算公式就是:
(FRotationMatrix(Rr) * FRotationMatrix(Rw)).Rotator()
注意:矩阵相乘时,两个乘数的前后位置不同则计算的结果也不同,比如上面例子,如果是( FRotationMatrix(Rot2) * FRotationMatrix(Rot1)).Rotator,则结果是Rotation(90, -90, -180)。
一个典型应用:以UE4为例,当角色移动时,不能将默认MoveForward的实参(比如(1.0, 0.f, 0.f))和MoveRight的实参(比如(0.0, 1.f, 0.f))传递给AddMovementInput,因为InputValue需要相对摄像机的朝向来计算,否则当按下W键,期望角色摄像机正对方向移动,但实际是侧向移动。此时就可以通过旋转矩阵相乘来获取当前摄像机朝向方向下的MoveForward和MoveRight方向。
FRotator AMyPlayerController::GetInputRotationInWorld() { FRotator Ret = FRotator::ZeroRotator; if (AMyCharacter* Player = Cast<AMyCharacter>(GetPawn())) { if(UCameraComponent* CameraComp = Player->GetFollowCamera()) { FRotator InputRotLS = FVector(ForwardInputValue, RighInputInputValue, 0.f).Rotation(); FRotator CameraRotWS = FRotator(0.f, CameraComp->GetComponentRotation().Yaw, 0.f); Ret = (FRotationMatrix(InputRotLS) * FRotationMatrix(CameraRotWS)).Rotator(); } } return Ret; }
Video Tutorials
Linear transformations and matrices | Essence of linear algebra, chapter 3
https://www.youtube.com/watch?v=kYB8IZa5AuE
六、抛物线Parabola movement
header
AStaticMeshActor* TestCube = nullptr; //throw speed UPROPERTY(EditDefaultsOnly) FVector StartForce = FVector(100.f, 100.f, 2000.f); //gravitational acceleration float GravityAcclerator = -980.f; //accumulated movtion time float AccumulateTime = 0.f;
cpp
void ATestTPGameMode::StartPlay() { Super::StartPlay(); //finding the Actor in scene. for (TActorIterator<AStaticMeshActor> Iter(GetWorld()); Iter; ++Iter) { if (Iter->GetName() == TEXT("Cube_2")) { TestCube = *Iter; break; } } } void ATestTPGameMode::Tick(float DeltaSeconds) { Super::Tick(DeltaSeconds); AccumulateTime += DeltaSeconds; //calculate gravitational speed in real time. float ZSpeed = GravityAcclerator * AccumulateTime; //calculate summation speed of gravitational speed and throw speed. FVector CurrSpeed = StartForce + FVector(0.f, 0.f, ZSpeed) ; //calculate movement distance in real time. FVector MoveDist = CurrSpeed * DeltaSeconds; //set relative location. TestCube->AddActorWorldOffset(MoveDist, true); }
七、空间点到直线垂足坐标的解算方法
算法1
原文:https://blog.csdn.net/zhouschina/article/details/14647587
假设空间某点O的坐标为(Xo,Yo,Zo),空间某条直线上两点A和B的坐标为:(X1,Y1,Z1),(X2,Y2,Z2),设点O在直线AB上的垂足为点N,坐标为(Xn,Yn,Zn)。点N坐标解算过程如下: 首先求出下列向量:
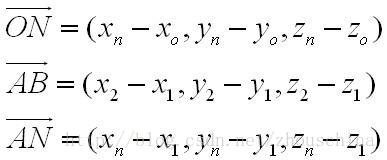
由向量垂直关系(公式1)
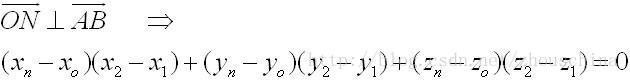
点N在直线AB上,根据向量共线(公式2):

由公式2得(公式3):
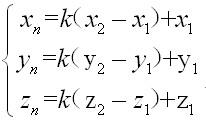
把公式3式代入公式1式,式中只有一个未知数k,整理化简解出k(公式4):
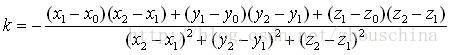
把公式4式代入公式3式即得到垂足N的坐标。
二维空间
// 二维空间点到直线的垂足 struct Point { double x,y; } Point GetFootOfPerpendicular( const Point &pt, // 直线外一点 const Point &begin, // 直线开始点 const Point &end) // 直线结束点 { Point retVal; double dx = begin.x - end.x; double dy = begin.y - end.y; if(abs(dx) < 0.00000001 && abs(dy) < 0.00000001 ) { retVal = begin; return retVal; } double u = (pt.x - begin.x)*(begin.x - end.x) + (pt.y - begin.y)*(begin.y - end.y); u = u/((dx*dx)+(dy*dy)); retVal.x = begin.x + u*dx; retVal.y = begin.y + u*dy; return retVal; }
三维空间
// 三维空间点到直线的垂足 struct Point { double x,y,z; } Point GetFootOfPerpendicular( const Point &pt, // 直线外一点 const Point &begin, // 直线开始点 const Point &end) // 直线结束点 { Point retVal; double dx = begin.x - end.x; double dy = begin.y - end.y; double dz = begin.z - end.z; if(abs(dx) < 0.00000001 && abs(dy) < 0.00000001 && abs(dz) < 0.00000001 ) { retVal = begin; return retVal; } double u = (pt.x - begin.x)*(begin.x - end.x) + (pt.y - begin.y)*(begin.y - end.y) + (pt.z - begin.z)*(begin.z - end.z); u = u/((dx*dx)+(dy*dy)+(dz*dz)); retVal.x = begin.x + u*dx; retVal.y = begin.y + u*dy; retVal.y = begin.z + u*dz; return retVal; }
算法2
原文:3D Perpendicular Point on Line From 3D point
https://stackoverflow.com/questions/9368436/3d-perpendicular-point-on-line-from-3d-point
计算p1、p2连成的直线上的离 q 点最近的点 f(即 q 点到直线 p1、p2的垂足坐标):
XNA实现
Vector3 p1 = new Vector3(x1, y1, z1); Vector3 p2 = new Vector3(x2, y2, z2); Vector3 q = new Vector3(x3, y3, z3); Vector3 u = p2 - p1; Vector3 pq = q - p1; Vector3 w2 = pq - Vector3.Multiply(u, Vector3.Dot(pq, u) / u.LengthSquared()); Vector3 f = q - w2;
UE4实现
FVector GetPerpendicularPointToLine(const FVector& PointStart, const FVector& PointEnd, const FVector& PointPerpendicular) { FVector Line = PointEnd - PointStart; FVector PS = PointPerpendicular - PointStart; FVector W2 = PS - (Line * (PS | Line) / Line.SizeSquared()); FVector FootPoint = PointPerpendicular - W2; return FootPoint; }
UE4引擎提供的工具函数:
FVector UKismetMathLibrary::FindClosestPointOnLine(FVector Point, FVector LineOrigin, FVector LineDirection) { const FVector SafeDir = LineDirection.GetSafeNormal(); const FVector ClosestPoint = LineOrigin + (SafeDir * ((Point-LineOrigin) | SafeDir)); return ClosestPoint; }
参考
Perpendicular on a line segment from a given point
https://stackoverflow.com/questions/10301001/perpendicular-on-a-line-segment-from-a-given-point
How do you find a point at a given perpendicular distance from a line?
https://stackoverflow.com/questions/133897/how-do-you-find-a-point-at-a-given-perpendicular-distance-from-a-line
八、已知三点求平面方程、平面法向量和点到平面的距离
原文:https://blog.csdn.net/zhouschina/article/details/8784908
已知三点p1(x1,y1,z1),p2(x2,y2,z2),p3(x3,y3,z3),要求确定的平面方程。
关键在于求出平面的一个法向量,为此做向量p1p2(x2-x1,y2-y1,z2-z1), p1p3(x3-x1,y3-y1,z3-z1),平面法线和这两个向量垂直,因此法向量n:
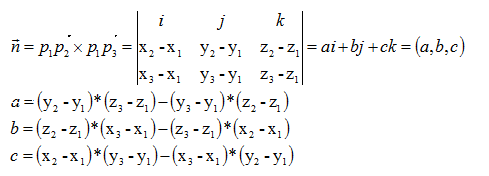
平面方程:
a * (x - x1) + b * (y - y1) + c * (z - z1) = 0; d = -a * x1 - b * y1 - c * z1;
平面方程2:
a * x + b * y + c * z + d=0;
代码:
//已知3点坐标,求平面ax+by+cz+d=0; void get_panel(Point p1, Point p2, Point p3, double &a, double &b, double &c, double &d) { a = ( (p2.y - p1.y) * (p3.z - p1.z) - (p2.z - p1.z) * (p3.y - p1.y) ); b = ( (p2.z - p1.z) * (p3.x - p1.x) - (p2.x - p1.x) * (p3.z - p1.z) ); c = ( (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x) ); d = ( 0 - (a * p1.x + b * p1.y + c * p1.z) ); } // 已知三点坐标,求法向量 Vec3 get_Normal(Point p1, Point p2, Point p3) { double a = ( (p2.y - p1.y) * (p3.z - p1.z) - (p2.z - p1.z) * (p3.y - p1.y) ); double b = ( (p2.z - p1.z) * (p3.x - p1.x) - (p2.x - p1.x) * (p3.z - p1.z) ); double c = ( (p2.x - p1.x) * (p3.y - p1.y) - (p2.y - p1.y) * (p3.x - p1.x) ); return Vec3(a, b, c); } //点到平面距离 double dis_pt2panel(Point pt, double a, double b, double c, double d) { return f_abs(a * pt.x + b * pt.y + c * pt.z + d) / sqrt(a * a + b * b + c * c); }
UE4提供的工具函数:
/** * Calculate the projection of a point on the plane defined by PlaneBase and PlaneNormal. * * @param Point The point to project onto the plane * @param PlaneBase Point on the plane * @param PlaneNorm Normal of the plane (assumed to be unit length). * @return Projection of Point onto plane */ static FVector FVector::PointPlaneProject(const FVector& Point, const FVector& PlaneBase, const FVector& PlaneNormal);
参考
三维凸包+点到平面距离+已知3点求平面方程
http://blog.csdn.net/pvpishard/article/details/7912511
Distance from point to plane
http://mathinsight.org/distance_point_plane
点到平面的垂足
http://blog.csdn.net/threewind/article/details/5980613