题目如下:
Given the
rootof a binary tree withNnodes, eachnodein the tree hasnode.valcoins, and there areNcoins total.In one move, we may choose two adjacent nodes and move one coin from one node to another. (The move may be from parent to child, or from child to parent.)
Return the number of moves required to make every node have exactly one coin.
Example 1:
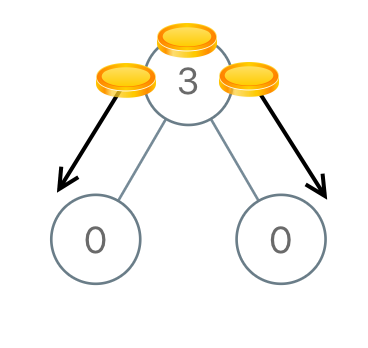
Input: [3,0,0] Output: 2 Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child.Example 2:
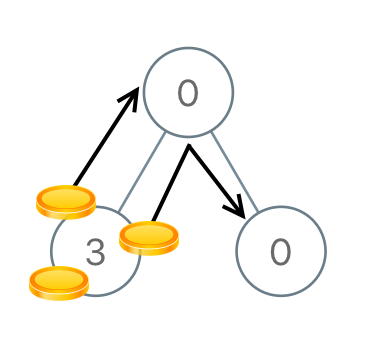
Input: [0,3,0] Output: 3 Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child.Example 3:
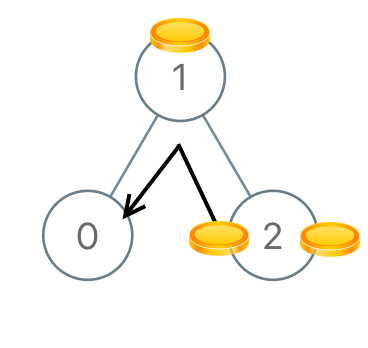
Input: [1,0,2] Output: 2Example 4:
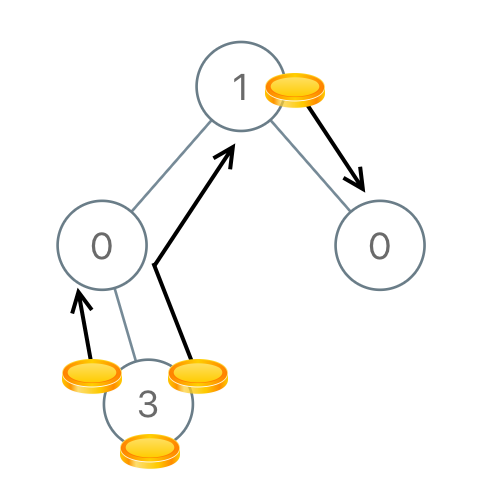
Input: [1,0,0,null,3] Output: 4Note:
1<= N <= 1000 <= node.val <= N
解题思路:这个题目有点意思,我的方法是“借”的思想。对于任意一个叶子节点,如果val是0,那么表示要向其父节点取一个coin,那么parent.val -= 1, moves += 1;如果是叶子节点的val大于1,那么表示要给父节点val-1个coin,同时moves += (val-1)。当然这两种情况可以用通用的表达式:move += abs(node.val - 1), parent.val += (node.val - 1)。按照后序遍历的方式即可算出总的move次数。
代码如下:
# Definition for a binary tree node. class TreeNode(object): def __init__(self, x): self.val = x self.left = None self.right = None class Solution(object): res = 0 def recursive(self,node,parent): if node.left != None: self.recursive(node.left,node) if node.right != None: self.recursive(node.right,node) self.res += abs(node.val - 1) if parent != None: parent.val += (node.val - 1) def distributeCoins(self, root): """ :type root: TreeNode :rtype: int """ self.res = 0 self.recursive(root,None) return self.res