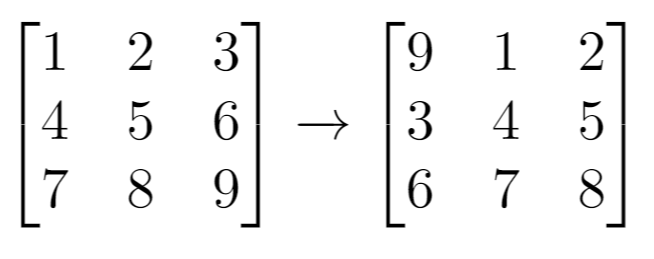题目如下:
Given a 2D
gridof sizen*mand an integerk. You need to shift thegridktimes.In one shift operation:
- Element at
grid[i][j]becomes atgrid[i][j + 1].- Element at
grid[i][m - 1]becomes atgrid[i + 1][0].- Element at
grid[n - 1][m - 1]becomes atgrid[0][0].Return the 2D grid after applying shift operation
ktimes.Example 1:
Input:grid= [[1,2,3],[4,5,6],[7,8,9]], k = 1 Output: [[9,1,2],[3,4,5],[6,7,8]]Example 2:
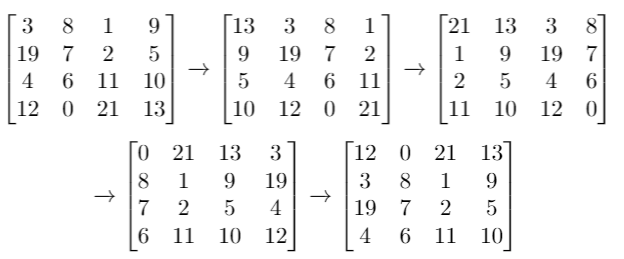
Input:grid= [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4 Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]Example 3:
Input:grid= [[1,2,3],[4,5,6],[7,8,9]], k = 9 Output: [[1,2,3],[4,5,6],[7,8,9]]Constraints:
1 <= grid.length <= 501 <= grid[i].length <= 50-1000 <= grid[i][j] <= 10000 <= k <= 100
解题思路:记grid的行数为row,列数为col,显然经过row*col次移动后和不移动效果是一样的,所以可以首先令k = k%(row*col)。剩下的k就是每一个元素需要移动的次数,我的方法是给grid的每个元素编号,从左到右,从上到下,依次为0,1,1....row*col - 1,这样方便计算。
代码如下:
class Solution(object): def shiftGrid(self, grid, k): """ :type grid: List[List[int]] :type k: int :rtype: List[List[int]] """ row = len(grid) col = len(grid[0]) k = k%(row * col) res = [[0] * col for _ in range(row)] for i in range(row): for j in range(col): inx = (i*col + j) + k if inx >= (row*col):inx -= row*col newrow = inx/col newcol = inx%col res[newrow][newcol] = grid[i][j] return res