【leetcode】1377. Frog Position After T Seconds

题目如下：

Given an undirected tree consisting of n vertices numbered from 1 to n. A frog starts jumping from the vertex 1. In one second, the frog jumps from its current vertex to another unvisited vertex if they are directly connected. The frog can not jump back to a visited vertex. In case the frog can jump to several vertices it jumps randomly to one of them with the same probability, otherwise, when the frog can not jump to any unvisited vertex it jumps forever on the same vertex. 

The edges of the undirected tree are given in the array edges, where edges[i] = [fromi, toi] means that exists an edge connecting directly the vertices fromi and toi.

Return the probability that after t seconds the frog is on the vertex target.

Example 1:

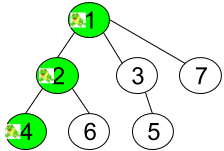
Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
Output: 0.16666666666666666 
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 probability to the vertex 2 after second 1 and then jumping with 1/2 probability to vertex 4 after second 2. Thus the probability for the frog is on the vertex 4 after 2 seconds is 1/3 * 1/2 = 1/6 = 0.16666666666666666. 

Example 2:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
Output: 0.3333333333333333
Explanation: The figure above shows the given graph. The frog starts at vertex 1, jumping with 1/3 = 0.3333333333333333 probability to the vertex 7 after second 1. 

Example 3:

Input: n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 20, target = 6
Output: 0.16666666666666666

Constraints:

• 1 <= n <= 100
• edges.length == n-1
• edges[i].length == 2
• 1 <= edges[i][0], edges[i][1] <= n
• 1 <= t <= 50
• 1 <= target <= n
• Answers within 10^-5 of the actual value will be accepted as correct.

解题思路：本题我用的是动态规划的方法、记dp[i][j]为j秒后青蛙位于第i个节点的概率。根据父子节点之间序号的关系，很容易了利用BFS方法将整个dp数组计算出来。但是有一点需要注意，如果节点i是叶子节点，并且能在第j秒到达，那么dp[i][t] = dp[i][j]。

代码如下：

class Solution(object):
    def frogPosition(self, n, edges, t, target):
        """
        :type n: int
        :type edges: List[List[int]]
        :type t: int
        :type target: int
        :rtype: float
        """
        dic = {}

        queue = [1]
        visit = [0] * len(edges)
        while len(queue) > 0:
            node = queue.pop(0)
            for i in range(len(edges)):
                if visit[i] == 1:
                    continue
                e1,e2 = edges[i][0],edges[i][1]
                if e1 == node:
                    dic[e1] = dic.setdefault(e1,[]) + [e2]
                    queue.append(e2)
                    visit[i] = 1
                elif e2 == node:
                    dic[e2] = dic.setdefault(e2, []) + [e1]
                    queue.append(e1)
                    visit[i] = 1

        #print dic

        dp = [[0] * (t+2) for _ in range(n+1)]
        dp[1][0] = 1
        queue = [(1,0)]

        while len(queue) > 0:
            node,time = queue.pop(0)
            if time > t:
                continue
            if node == 3 and time == 2:
                pass
            if node not in dic:
                continue
            for child in dic[node]:
                dp[child][time+1] = float(dp[node][time])/float(len(dic[node]))
                queue.append((child,time+1))

        res = dp[target][t]
        if dp[target][t] == 0 and target not in dic:
            for i in range(t,-1,-1):
                if dp[target][i] != 0:
                    res = dp[target][i]
                    break
        #print dp
        return res