【leetcode】1514. Path with Maximum Probability

题目如下：

You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].

Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.

If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5. 

Example 1:

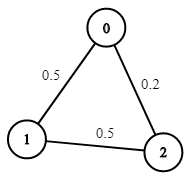
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
Output: 0.25000
Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.

Example 2:

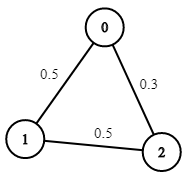
Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
Output: 0.30000

Example 3:

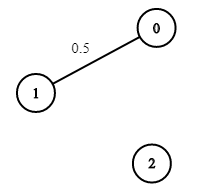
Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
Output: 0.00000
Explanation: There is no path between 0 and 2. 

Constraints:

• 2 <= n <= 10^4
• 0 <= start, end < n
• start != end
• 0 <= a, b < n
• a != b
• 0 <= succProb.length == edges.length <= 2*10^4
• 0 <= succProb[i] <= 1
• There is at most one edge between every two nodes.

解题思路：采用BFS的方法，从start开始，依次可以把能到达的节点加入队列中，加入队列之前需要判断通过当前路径到达节点的几率是否比之前其他路径的几率大，只有大于的情况，才能把节点加入队列。

代码如下：

class Solution(object):
    def maxProbability(self, n, edges, succProb, start, end):
        """
        :type n: int
        :type edges: List[List[int]]
        :type succProb: List[float]
        :type start: int
        :type end: int
        :rtype: float
        """
        dic = {}
        dic_succ = {}
        for i in range(len(edges)):
            e1, e2 = edges[i]
            dic_succ[(e1,e2)] = succProb[i]
            dic[e1] = dic.setdefault(e1,[]) + [e2]
            dic[e2] = dic.setdefault(e2,[]) + [e1]

        max_prob = [0.0] * n
        max_prob[start] = 1
        queue = [start]
        while len(queue) > 0:
            node = queue.pop(0)
            prob = max_prob[node]
            if node not in dic:continue
            elif node == end:
                continue
            for next_node in dic[node]:
                edge_prob = dic_succ[(node,next_node)] if (node,next_node) in dic_succ else dic_succ[(next_node,node)]
                if prob * edge_prob > max_prob[next_node]:
                    max_prob[next_node] = prob * edge_prob
                    queue.append(next_node)
        return max_prob[end]