题目如下:
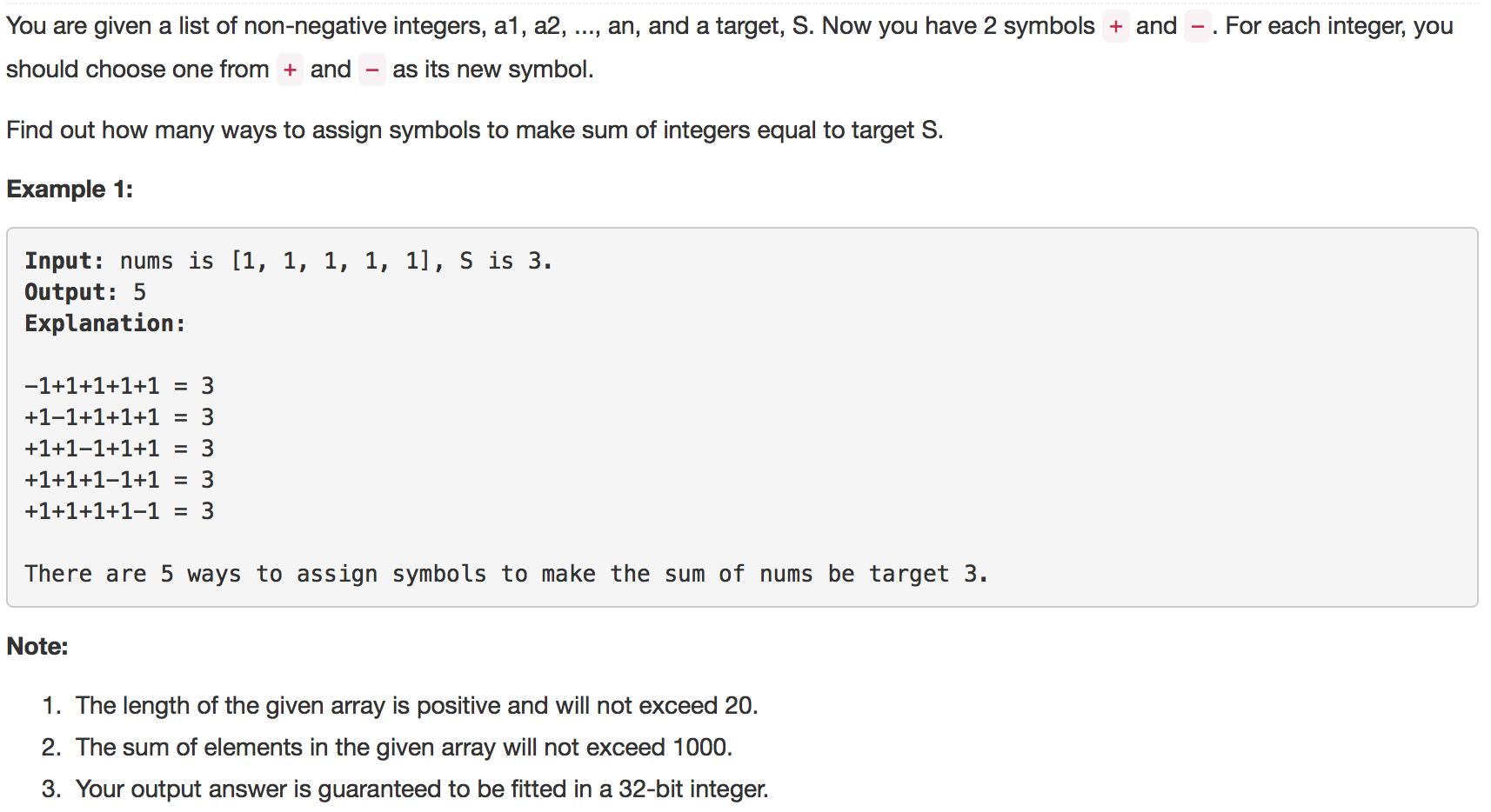
解题思路:这题可以用动态规划来做。记dp[i][j] = x,表示使用nums的第0个到第i个之间的所有元素得到数值j有x种方法,那么很容易得到递推关系式,dp[i][j] = dp[i-1][j - nums[i]] + dp[i-1][j + nums[i]]。考虑到j可以为负数,因为j的取值范围是[-sum(nums) ,sum(nums)],为了保证在dp数组中的j一直为正数,我们做一个数组的向右平移,平移sum(nums)的长度,即把-sum(nums) 移动到0。
代码如下:
class Solution(object): def findTargetSumWays(self, nums, S): """ :type nums: List[int] :type S: int :rtype: int """ Amount = sum(nums) if S > Amount or S < -Amount: return 0 MaxValue = max(nums) dp = [[0 for x in xrange(2*(Amount+MaxValue)+1)] for x in nums] dp[0][nums[0] + Amount] += 1 dp[0][-nums[0] + Amount] += 1 for i in xrange(1,len(dp)): for j in xrange(-Amount,Amount+1): dp[i][j + Amount] = dp[i - 1][j - nums[i]+ Amount] + dp[i - 1][j + nums[i] + Amount] #print dp return dp[len(nums)-1][S+ Amount]