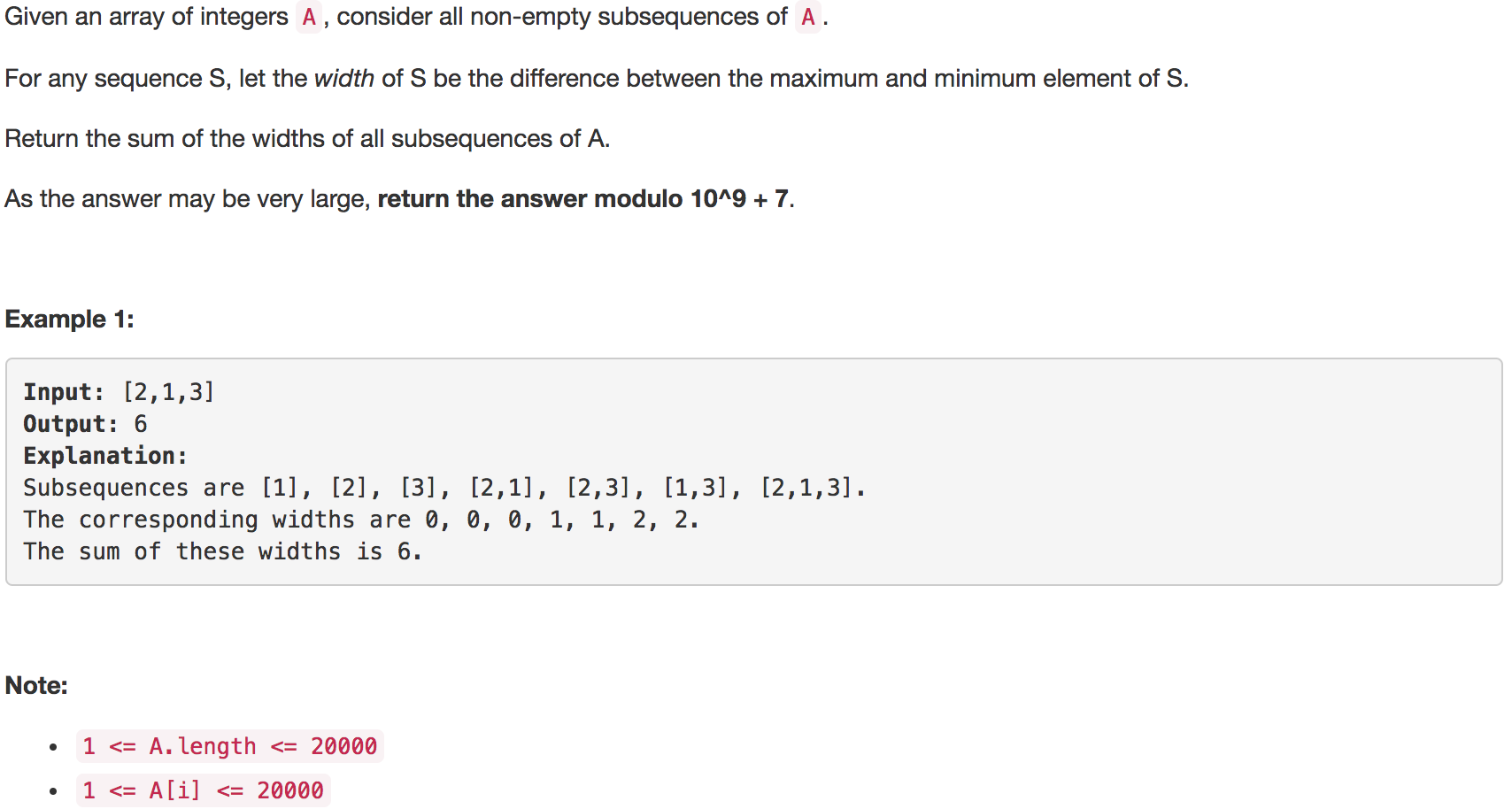
题目如下:
解题思路:题目定义的子序列宽度是最大值和最小值的差,因此可以忽略中间值。首先对数组排序,对于数组中任意一个元素,都可以成为子序列中的最大值和最小值而存在。例如数组[1,2,3,4,5,6],对于元素3来说,由左边[1,2]组成的所有子序列都可以以3为最大值的,而右边[4,5,6]组成的所有子序列都可以以3为最小值。根据排列组合的原理:[1,2]可以组成的子序列个数为C(2,1) + C(2,2) ,而[4,5,6]可以组成的子序列个数为C(3,1) + C(3,2) + C(3,3) ,同样根据组合计算定律,C(n,1) + C(n,2) + ...... + C(n,n) = 2^n - 1。因为以3为最大值是做被减数,以3为最小值是做减数,因此以3作为最大/最小值的所有子序列的和宽度和就是:(2 ^ 2 - 1)* 3 - (2 ^ 3-1)*3 。同理,也可以求出其他元素的宽度和,并最终求出总宽度和。根据组合的对称性,C(n,m) = C(n,n-m),因此只需要遍历一半的数组长度即可。
代码如下:
class Solution(object): def sumSubseqWidths(self, A): """ :type A: List[int] :rtype: int """ A.sort() res = 0 l = 1 r = pow(2, len(A) - 1) for i in range(len(A)/2): res += l * A[i] res -= r * A[i] res += r * A[len(A)-i-1] res -= l * A[len(A) - i - 1] l *= 2 r /= 2 return res % (pow(10,9) + 7)