插值与拟合的概念
首先对两种说法进行阐明。
插值:做一条指定类型的曲线(如多项式),使其通过所有数据点。
拟合:做一条指定类型的曲线,使其在一定意义下逼近该组数据点。
两种概念的不同,可以看到,对于插值,很可能会出现对所有数据点都通过,但是并不一定很好的拟合真实数据的情况。
几种常见插值方法
下给定如下插值的数学语言表示:
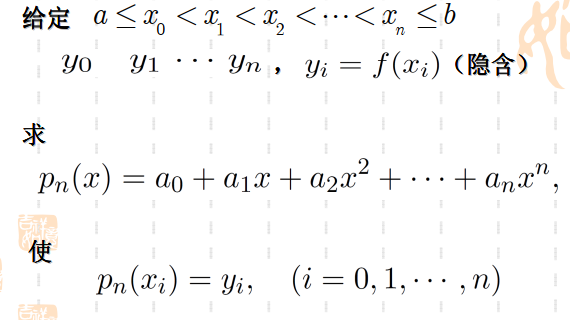
代数多项式插值
Lagrange插值
Lagrange插值是一种线性插值,其具体定义如下:
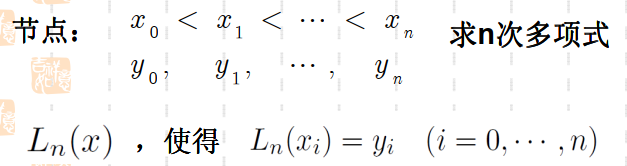
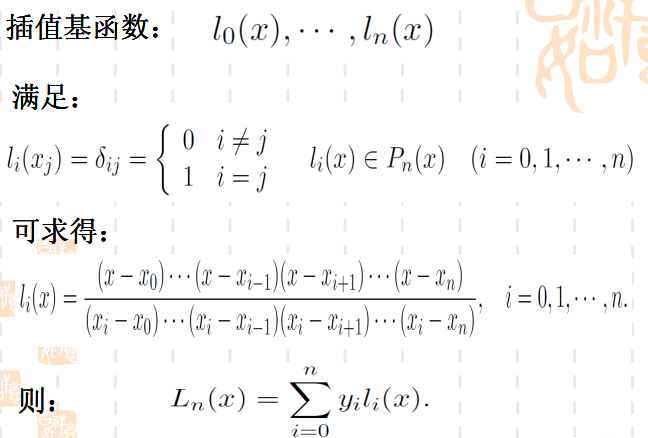
上述定义含义,即Lagrange插值是构造一个线性多项式,使得通过所有的数据点。
此外,根据定义,Lagrange插值存在着缺陷:如果数据点增加,就需要重新计算插值基函数。
Newton插值
Lagrange插值存在的缺点,Newton插值借助差商来优化。
那么什么是差商呢?


由差商概念,引出Newton插值公式为:
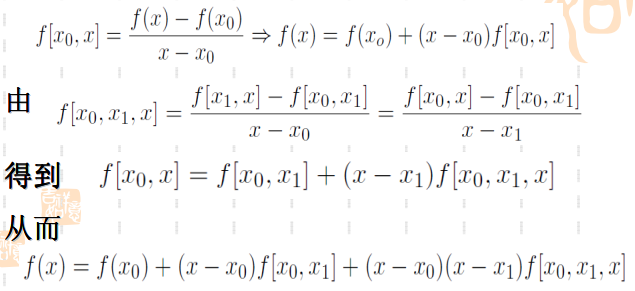

借用这种方式,即使节点增加,原计算结果仍有用,新节点的计算借助于原节点的差商结果。
Hermite插值

分段插值
由于Lagrange高次多项式插值存在Runge现象,这个会在后面说明。为了缓解这一问题,采用分段低次插值。
分段线性插值
分段线性插值的基本思想实际上是用一个低次分段函数来插值两个数据点。

分段抛物插值

分段三次Hermite保形插值
该方法有要求限定,即需要在分段点处连续可导。然后再每两个相邻数据点之间采用三次Hermite插值。
三次样条插值
样条插值的曲线是二阶导数连续的插值曲线,其定义为:


等距插值的问题----Runge现象
对于等间距插值,会引发Runge现象,在mathmatic中运行下图程序,具体表现为:
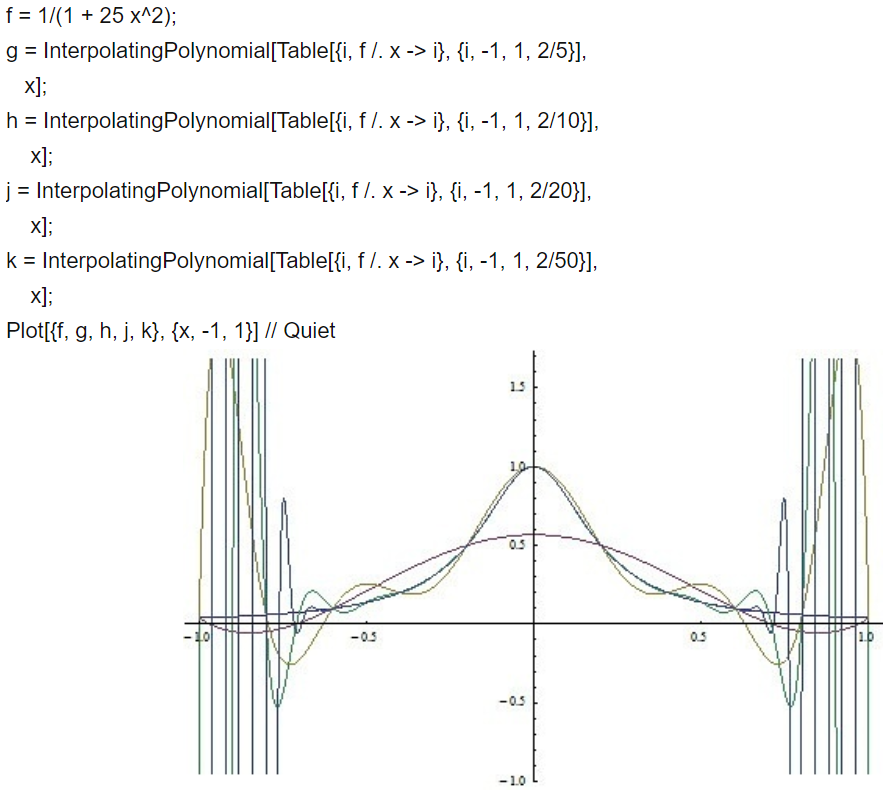
可以看到,在边缘处,会产生震荡,难以拟合整个函数曲线,且数据点越多,震荡越剧烈。可见多项式插值并不能很好的收敛到函数本身。
几种常见插值的python实现
代码后面补上。