译文转:https://blog.csdn.net/alihouzi/article/details/45190303
原文转:http://users.rowan.edu/~polikar/WTpart1.html
三、为什么我们需要频率信息(1)?
通常,我们可以容易的从频域中看到一些在时域中看不到的信息。
让我们举一个生物信号的例子。假如我们正在观看一个心电图,心脏病专家一般都熟知一些典型的健康心电图。如果某个心电图与一般的心电图有较大的偏差,这往往是发病的征兆。
在心电图的时域信号中一般很难找到这些病情。心脏病专家们一般用记录在磁带上的时域心电图来分析心电信号。最近,新的心电记录仪/分析仪还可以提供心电图的频域信息,通过这些信息,他们就可以确定病症是否存在。对频域图进行分析能使他们更容易的诊断病情。
上面只是一个说明了为何频率幅值有用的简单例子。当前,傅立叶变换已经被用于不同的领域,这些领域包括工程学的各个分支。
虽然傅立叶变换是最流行的数学变换,但它并不是唯一的。工程师和数学家们还经常会用到很多其他的变换。如希尔伯特变换、短时傅立叶变换(后文对此有详细阐述)、魏格纳分布和雷登变换,当然还有我们要讲的特征变换——小波变换。这些变换只不过是工程师和数学家们所用到的变换中的一小部分。每一种变换都有自己的应用领域,也都各有优缺点,小波变换也不例外。
为了更好的理解小波变换的必要性,让我们更详细的探讨一下傅立叶变换。傅立叶变换是一种可逆变换,即它允许原始信号和变换过的信号之间互相转换。不过,在任意时刻只有一种信息是可用的,也就是说,在傅立叶变换后的频域中不包含时间信息,逆变换后的时域中不包含时间信息。说到这里,脑袋里很自然的就会提出这个问题,有没有一种变换可以同时提供时间和频率信息呢?
我们马上就会知道,答案是具体问题具体分析。回想一下,傅立叶变换给出了信号中包含的频率信息,即它可以告诉我们原始信号中不同频率的信号到底有多少,但是并没有告诉我们某个频率信号是在何时出现的。在处理平稳信号时,我们不需要知道这些。
让我们进一步探讨一下平稳这个概念,因为它在信号分析中具有重要意义。如果某个信号中的频率分量一直保持不变,则我们叫这类信号为平稳信号。换句话说,静态信号中的频率分量一直保持不变。这种情况下,就不需要知道频率分量是什么时候出现的,因为所有的频率分量出现在信号的每一刻!!!
以下面这个信号为例:
x(t)=cos(2*pi*10*t)+cos(2*pi*25*t)+cos(2*pi*50*t)+cos(2*pi*100*t)
这是一个平稳信号,因为频率为10,25,50和100Hz的频率分量出现在整个时域内。如下图所示:
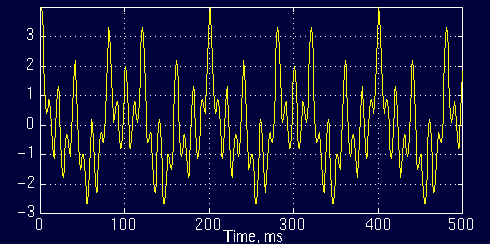
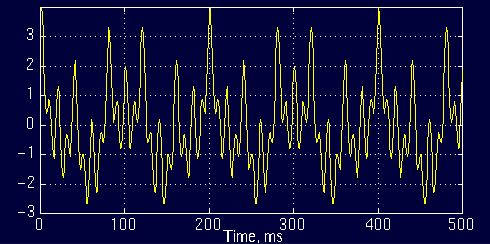
图1.5
下图为它的傅立叶变换:

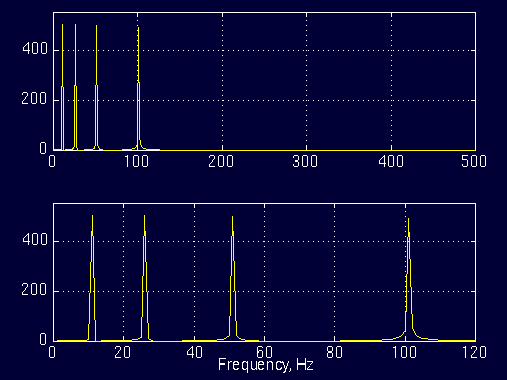
图1.6
图1.3中的上图是图1.2的频谱图,下图为上图的放大,仅仅显示了我们感兴趣部分的频率信息。四个频谱分量分别对应着10,25,50和100Hz。
与图1.3不同,下图所示的信号就是一个非平稳的信号。图1.4所示的信号,它的频率一直在改变,这种信号被称为变频信号,是一种非平稳信号。

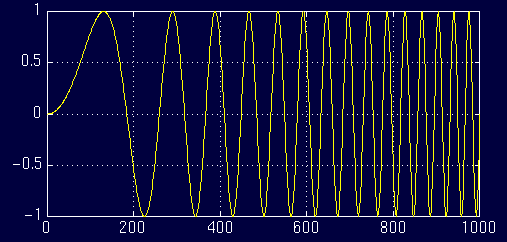
图1.7
让我们再看一个例子,图1.5显示了一个包含四个频率分量的信号,它们分别在不同时刻出现,因此这是一个非平稳信号。0-300ms时是一个100Hz的正弦波,300-600ms时则是一个50Hz的正弦波,600-800ms时是一个25Hz的正弦波,最后的200ms内是一个10Hz正弦波。

图1.8
下图是它的傅立叶变换:

图1.9
不要担心图中出现那些毛刺,那是由于信号中频率的突变引起的,在这篇文章里这些没有意义。注意到那些高频分量的幅度比低频分量大,这是因为高频信号比低频信号持续时间更长一些(分别为300ms和200ms)(信号中各频率分量的确切值并不重要)。
除了那些毛刺,图中的一切看起来都是正常的,有四个尖峰,对应原始信号中的四个频率分量,应该是正确的…
错!
当然了,也不完全错,但起码不完全对。对图1.5,考虑以下问题:各个频率分量都是在什么时刻出现的?
答案是
在所有时刻!还记得平稳信号吗?所有频率分量在信号的整个周期内一直存在,10Hz的信号一直存在,50Hz的信号亦然,100Hz的信号亦然。
现在,让我们来考虑一下图1.7或1.8展示的非平稳信号。
各个频率分量都是在什么时刻出现的?
对于图1.6来说,我们知道,在第一个时间段内出现的是最高频率的分量,在最后一个时间段内出现的是最低频率的分量。图1.5中信号的频率分量一直在变,因此,对这些信号来说,各个频率分量并没有出现在任意时刻。
现在,比较一下图1.6和1.9,二者的相似之处是显而易见的,在图中都显示了四个几乎一样的频率分量,即10,25,50和100Hz。除了1.6中的那些毛刺和两幅图中各频率分量的幅值(这些幅值可以做归一化处理),两幅频谱图几乎是一致的,虽然相应的时域信号之间差别很大。两个信号都包含了相同的频率分量,但是前者中的各频率分量出现在信号的整个周期内,而后者的频率分量则在不同的时间段内出现。那么,是什么导致两个完全不同的原始信号经傅立叶变换后的波形这么相像呢?回想一下,傅立叶变换仅仅给出了信号的频谱分量,但是却没有给出这些频谱分量的出现时间。因此,对于非平稳信号来说,傅立叶变换是不合适的,但有一个例外:
只有当我们仅仅关心信号中是否包含某个频率分量而不关心它出现的时间的时候,傅立叶变换才可以用于处理非平稳信号。但是,如果这些信息是我们需要的(假设),如果我们想知道频率分量出现的确切时间,傅立叶变换就不是合适的选择了。
对实际应用来说,很难把两者的区分开来,因为现实中平稳的和非平稳的信号都很多。举例来说,几乎所有的生物信号都是非平稳的,这其中著名的就是心电图(ECG)、脑电图(EEG)和肌电图(EMG)。
请注意,傅立叶变换仅仅给出了信号的频率分量信息,仅此而已,无它。
当需要对频谱分量进行时间定位时,则需要一个可以得到信号的时频表示的数学变换。