Matlab smooth函数原理

由于项目上要用到平滑一维数组数据，参考Matlab  smooth函数转成c++代码

// x,g均为数组，具体内容略
plot(x,g);hold on,plot(x,smooth(g,50),'r');
z1 = (g1-smooth(g1,50)');  figure,plot(x,z1,'.-')

蓝色为平滑前，红色为平滑后

为了要找到缺陷，即灰度值突变很大地方，可以平滑前后相减，注意这里平滑窗宽尽量选大，选择原则是较小甚至不影响缺陷突变的地方

    平滑前后相减

                     

举例

例如g=[1 2 1 5 1 1 1 3 1 1 1]

smooth(g,5)'

ans =

1.0000    1.3333    2.0000    2.0000    1.8000    2.2000    1.4000    1.4000    1.4000    1.0000    1.0000

smooth(g,10)'

ans =

    1.0000    1.3333    2.0000    1.7143    1.7778    1.7778    1.6667    1.2857    1.4000    1.0000    1.0000

以窗宽10为例(因为除的奇数，所以最大为9)  (matlab 下标以1开始,而vc从0开始)

令b=(k-1)/2;

当i小于b时    

Y[0]=g[0] =1

Y[1]=(g[0]+g[1]+g[2])/3=4/3=1.3333

Y[2]=(g[0]+g[1]+g[2]+g[3]+g[4])/5=2

Y[3]=(g[0]+g[1]+g[2]+g[3]+g[4]+g[5]+g[6])/7=1.7143 

Y[3]= (g[3+(-3)]+g[3+(-2)]+g[3+(-1)]+g[3+(0)]+g[3+1]+g[3+2]+g[3+3])/(2*3+1)

那么从j=-i：i    (这里k是变动的)

Y[i]=0;

   For( j=-i;j<i+1;i++)

{

      Y[i]+=g[i+j]

}

Y[i]=y[i]/(2*i+1);

当i大于等于时 ，同时length(g)-i>b  (这里k是固定的)

如果n为偶数，那么应该是k=n-1；然后范围是-(k-1)/2: (k-1)/2   b=(k-1)/2

Y[4]=(g[0]+g[1]+g[2]+g[3]+g[4]+g[5]+g[6] +g[7]+g[8])/9=1.7778

Y[5]=(g[1]+g[2]+g[3]+g[4]+g[5]+g[6] +g[7]+g[8] +g[9])/9=1.7778

Y[6]=(g[2]+g[3]+g[4]+g[5]+g[6]+g[7]+g[8] +g[9]+g[10])/9=1.6667

Y[6]= (g[6+(-4)]+g[6+(-3)]+g[6+(-2)]+g[6+(-1)]+g[6]+g[7]+g[8] +g[9]+g[10])/9…..

Y[i]=(g[i+(-b)]+g[i+(-b+1)]+g[i+(-b+2)]+g[i+(-b+3)]+g[i+(-b+4)]+g[i+(-b+5)]+g[i+(-b+6)] +g[i+(-b+7)]+g[i+(-b+8)])/k

-b：b即

If(i>b)||(i=b)

{

   Y[i]=0;

   For( j=-b;j<b+1;b++)

{

      Y[i]+=g[i+j]

}

Y[i]=y[i]/k;}

当i大于b  同时 length(g)-i<=b   从后往前推

Y[7]=( g[4]+ g[5]+g[6] +g[7]+g[8] +g[9]+g[10])/7=1.2857

Y[8]=( g[6] +g[7]+g[8] +g[9]+g[10])/5=1.4

Y[9]=( g[8] +g[9]+g[10])/3=1

Y[10]=(g[10] =1

当i=7时，i1=10-7=3

那么Y[7]= (g[7+(-3)]+g[7+(-2)]+g[7+(-1)]+g[7+(0)]+g[7+1]+g[7+2]+g[7+3])/(2*3+1)

当i=8时，i1=2

那么Y[8]= (g[8+(-2)]+g[8+(-1)]+g[8+(0)]+g[8+1]+g[8+2])/(2*2+1)

令 i1=(n-1)-i,那么从-i1：i1

Y[i]=0;

   For( j=-i1;j<i1+1;i1++)

{

      Y[i]+=g[i+j]

}

Y[i]=y[i]/(2*i1+1);

 

C++代码如下，nn为数组元素个数；

            int b=(k-1)/2;
            vector<double> Z(nn);
            if(nn>k)
            {
                for(int i=0;i<nn;i++)
                {

                    if(i<b)
                    {
                        Z[i]=0;
                        for(int j=-i;j<i+1;j++)
                        {
                            Z[i]+=D[i+j];
                        }
                        Z[i]=Z[i]/(2*i+1);
                    }
                        
                  else  if(((i>b)||(i=b))&((nn-i)>b))
                    {
                        Z[i]=0;
                        for( int j=-b;j<b+1;j++)
                        {
                            Z[i]+=D[i+j];
                        }
                        Z[i]=Z[i]/k;
                    }
                    else
                    {
                        Z[i]=0;
                        int i1=(nn-1)-i;
                        for( int j=-i1;j<i1+1;j++)
                        {
                            Z[i]+=D[i+j];
                        }
                        Z[i]=Z[i]/(2*i1+1);
                    }
                }
            }

  平滑前

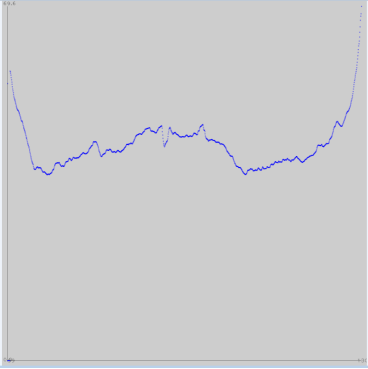
 平滑后

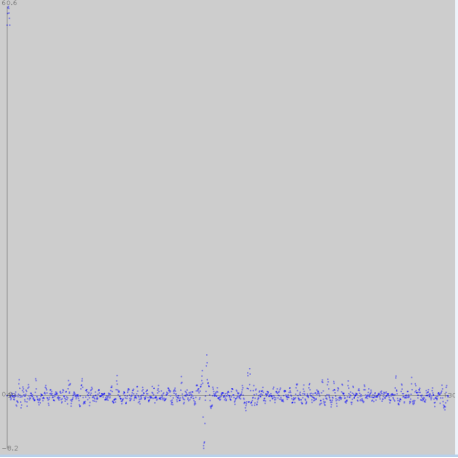
 平滑前后相减