关于贝塞尔曲线

https://www.cnblogs.com/hnfxs/p/3148483.html

https://blog.csdn.net/Dang_boy/article/details/84570221

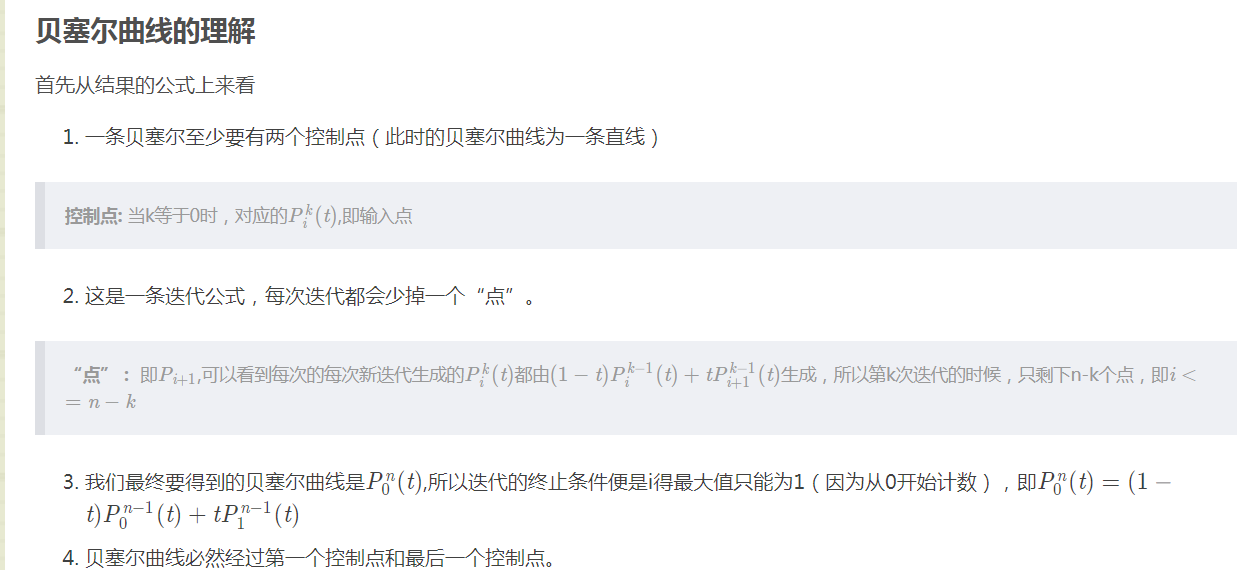
原理和简单推导（以三阶为例）：

设P₀、P₀²、P₂是一条抛物线上顺序三个不同的点。过P₀和P₂点的两切线交于P₁点，在P₀²点的切线交P₀P₁和P₂P₁于P₀¹和P₁¹，则如下比例成立：

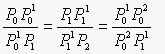
这是所谓抛物线的三切线定理。

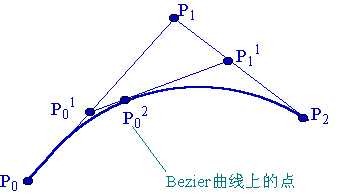
当P₀，P₂固定，引入参数t，令上述比值为t:(1-t)，即有：

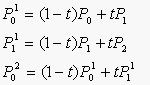
t从0变到1，第一、二式就分别表示控制二边形的第一、二条边，它们是两条一次Bezier曲线。将一、二式代入第三式得：

 

当t从0变到1时，它表示了由三顶点P₀、P₁、P₂三点定义的一条二次Bezier曲线。

并且表明：

这二次Bezier曲线P₀²可以定义为分别由前两个顶点(P₀,P₁)和后两个顶点(P₁,P₂)决定的一次Bezier曲线的线性组合。

依次类推，

由四个控制点定义的三次Bezier曲线P₀³可被定义为分别由(P₀,P₁,P₂)和(P₁,P₂,P₃)确定的二条二次Bezier曲线的线性组合，由(n+1)个控制点P_i(i=0,1,...,n)定义的n次Bezier曲线P₀ⁿ可被定义为分别由前、后n个控制点定义的两条(n-1)次Bezier曲线P₀^n-1与P₁^n-1的线性组合：

由此得到Bezier曲线的递推计算公式

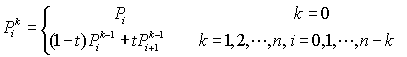
这就是这就是de Casteljau算法，可以简单阐述三阶贝塞尔曲线原理。

下面是总结：转自http://blog.csdn.net/tianhai110/article/details/2203572

Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线。 曲线定义：起始点、终止点（也称锚点）、控制点。通过调整控制点，贝塞尔曲线的形状会发生变化。 1962年，法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法，并给出了详细的计算公式，因此按照这样的公式绘制出来的曲线就用他的姓氏来命名，称为贝塞尔曲线。

以下公式中：B(t)为t时间下 点的坐标；

P₀为起点,P_n为终点,P_i为控制点

一阶贝塞尔曲线(线段)：

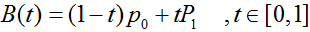
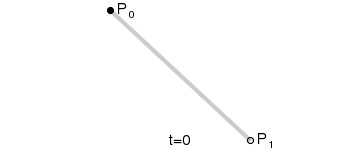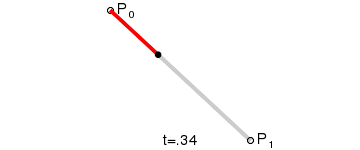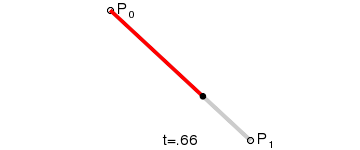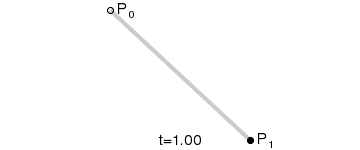
意义：由 P0 至 P1 的连续点， 描述的一条线段

二阶贝塞尔曲线(抛物线)：

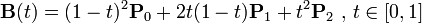
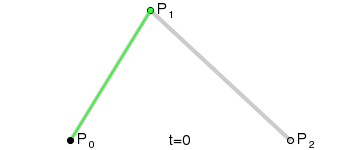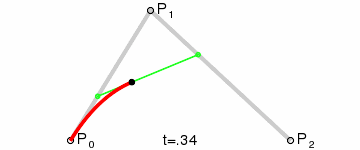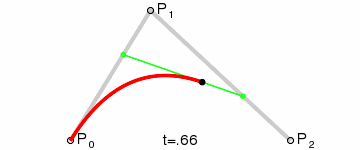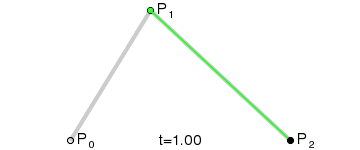
原理：由 P0 至 P1 的连续点 Q0，描述一条线段。
      由 P1 至 P2 的连续点 Q1，描述一条线段。
      由 Q0 至 Q1 的连续点 B(t)，描述一条二次贝塞尔曲线。

经验：P1-P0为曲线在P0处的切线。

三阶贝塞尔曲线：

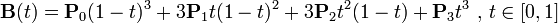
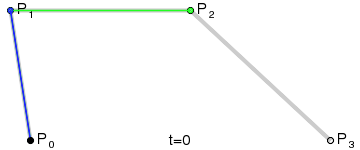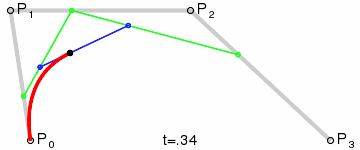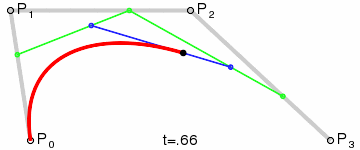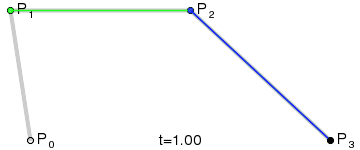
通用公式：

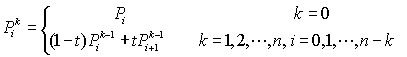
高阶贝塞尔曲线：

4阶曲线：

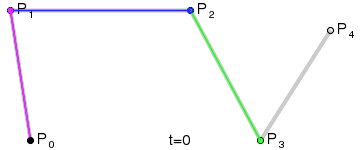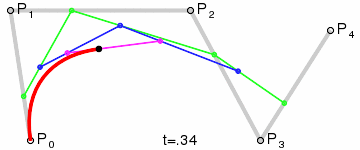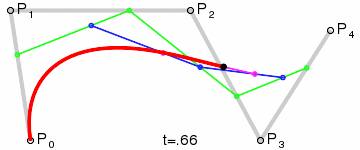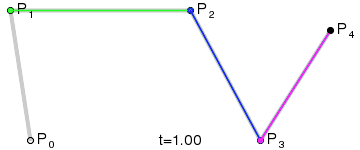
5阶曲线：

第二篇博文:

 

 

#include <iostream>
#include <opencv2/opencv.hpp>
#include <vector>
using namespace cv;
using std::cout;
using std::endl;
using std::vector;
vector<Point2f> bezierCurve(vector<Point2f> src);
int main(int argc, char const* argv[])
{
   while (1) {
       vector<Point2f> path;
       CvRNG rng;
       rng = cvRNG(cvGetTickCount());
       for (int i = 1; i < 6; i++)
           path.push_back(Point2f(i * 800 / 6.0, cvRandInt(&rng) % 800));

       Mat img(800, 800, CV_8UC3);
       img = 0;
       for (int i = 0; i < path.size(); i++)
           circle(img, path[i], 3, Scalar(0, 0, 255), 3); //BGR
       vector<Point2f> bezierPath = bezierCurve(path);
       for (int i = 0; i < bezierPath.size(); i++) {
           //circle(img, bezierPath[i], 3, Scalar(0, 255, 255), 3); //BGR
           img.at<cv::Vec3b>(cvRound(bezierPath[i].y), cvRound(bezierPath[i].x)) = { 0, 255, 255 };
       }
       imshow("black", img);
       if (waitKey(0) == 'q')
           break;
   }
   return 0;
}
vector<Point2f> bezierCurve(vector<Point2f> src)
{
   if (src.size() < 1)//这种情况是不允许出现的，出现只能证明程序出错了
       return src;
   const float step = 0.01;//采集100个点，即1.0/step
   vector<Point2f> res;
   if (src.size() == 1) {//递归结束条件，k=0
       for (float t = 0; t < 1; t += step)
           res.push_back(src[0]);//为了和其他情况保持一致，生成了1.0/step个一样的点
       return res;
   }
   vector<Point2f> src1;
   vector<Point2f> src2;
   src1.assign(src.begin(), src.end() - 1);//分成两部分，即Pi和Pi+1
   src2.assign(src.begin() + 1, src.end());
   for (int i = 0; i < src1.size(); i++)
       cout << src1[i] << endl;
   cout << endl;
   for (int i = 0; i < src2.size(); i++)
       cout << src2[i] << endl;
   cout << endl;
   vector<Point2f> pln1 = bezierCurve(src1);
   vector<Point2f> pln2 = bezierCurve(src2);
   for (float t = 0; t < 1; t += step) {
       Point2f temp;
       temp = (1.0 - t) * pln1[cvRound(1.0 / step * t)] + t * pln2[cvRound(1.0 / step * t)];
       res.push_back(temp);
   }
   return res;
}

实现效果