为什么将样本方差除以N1?

偶然间发现了一个博客，讲了一些数学基础知识————方差、协方差等。为防止半途而废，在此翻译，水平不足，尽量做好！
原文：https://www.visiondummy.com/2014/03/divide-variance-n-1/

前言

在本文中，我们将推导计算正态分布数据的均值和方差的著名公式，以回答文章标题中的问题。然而，对于那些对这个问题的“为什么”不感兴趣，而只对“何时”感兴趣的读者来说，答案很简单：
如果必须同时估计数据的平均值和方差（通常情况下），则除以N-1，得出方差为：

另一方面，如果真实总体的均值已知，只需要估计方差，则除以 N，得到方差为：

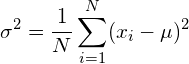
前者是您通常需要的，后者的一个例子是高斯白噪声分布的估计。由于已知高斯白噪声的平均值为零，因此在这种情况下只需估计方差。
如果数据是正态分布的，我们可以完全用它的均值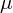和方差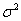来描述它。方差是标准偏差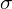的平方，代表每个数据点与平均值的平均偏差。换句话说，方差表示数据的离散。对于正态分布数据，68.3%的观测值介于和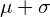之间。下图显示了具有均值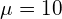和方差的高斯密度函数：

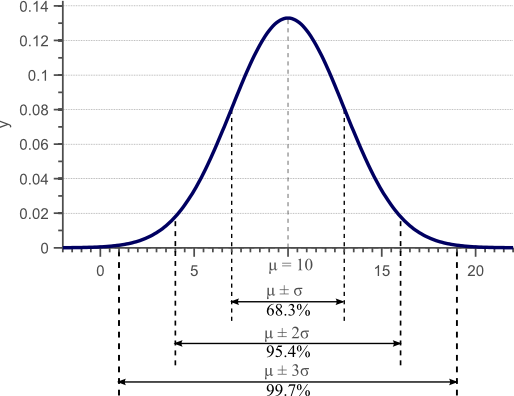
图表1 高斯密度函数。对于正态分布的数据，68% 的样本落在平均值加减标准差定义的区间内

通常我们无法访问全部数据。在上面的例子中，我们通常会有一些观察结果供我们使用，但我们无法访问定义绘图x轴的所有可能观察结果。例如，我们可能有以下一组观察结果：
表格1

观察ID	观察值
观察1	10
观察2	12
观察3	7
观察4	5
观察5	11

如果我们现在通过将所有值相加并除以观察次数来计算经验平均值，我们有：

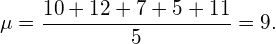\tag{1}

通常我们假设经验平均值接近分布的实际未知平均值，因此假设观测数据是从具有平均值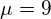的高斯分布中采样的。在本例中，分布的实际平均值为10，因此经验平均值确实接近实际平均值。
数据的方差计算如下：

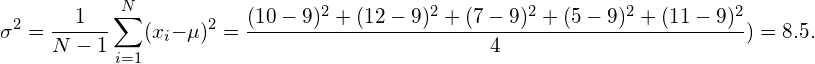\tag{2}

同样，我们通常假设这种经验方差接近于潜在分布的真实和未知方差。在本例中，实际方差为9，因此经验方差确实接近实际方差。现在的问题是，为什么用于计算经验平均值和经验方差的公式是正确的。事实上，计算方差的另一个常用公式定义如下：
现在的问题是为什么用于计算经验均值和经验方差的公式是正确的。事实上，另一个常用的计算方差的公式，定义如下：
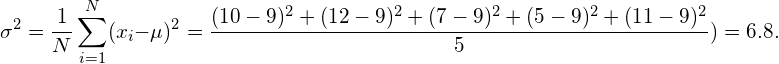\tag{3}