一、
范德蒙矩阵的形式
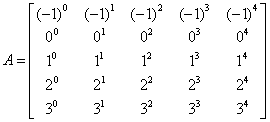
二、代码如下
范德蒙矩阵
x=[-1 0 1 2 3]'; %定义5维列向量x
for i=1:1:5 %行控制变量i从1~5,步长为1
for j=1:1:5 %列控制变量j从1~5,步长为1
A(i,j)=x(i)^(j-1); %对矩阵元素A(i,j)赋值
end
end
三、matlab自有代码
vander
todo:以后再了解吧
四、嘿嘿嘿,得来全不费工夫
上午不了解的问题,偶然之间竟然发现了解决办法,赶紧来记录一下
从行列式开始
范德蒙行列式是长这个样子滴:
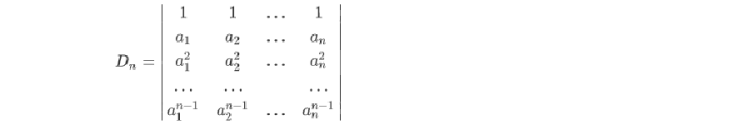
然后呢,它的转置也叫做范德蒙行列式:

为什么呢?
因为矩阵转置,行列式的值不会变
这里我就不推导了,直接给出范德蒙行列式的值:

这是什么意思呢?
假设有如下的范德蒙方阵:

那么它的行列式等于:(3-2)(5-2)(5-3)=6
假设4阶范德蒙行列式中有四个数2,3,5,7那么就等于(3-2)(5-2)(7-2)(5-3)(7-3)(7-5)=240
考试中经常出现与范德蒙行列式类似的结构,它们就差了那么一点点,我们需要做的就是将之转化为
标准的范德蒙行列式便于计算。这里我举一个例子。

上面这个行列式长得太像范德蒙矩阵了,只是没有三次项,我们给它补上。

这里除了补上三次项,还有未知数x,为什么呢?当然首先是只有方阵才有行列式。
这样整个行列式的值为:
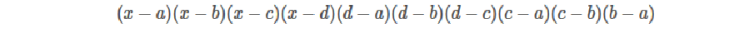
我们仅看 x^3 项的系数(负的原行列式的值)就是答案:
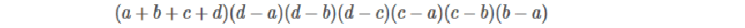
怎么理解呢?原因就是代数余子式按列展开等于行列式的值
(1,x,x2,x3,x4)T按列展开一次得到对应级次的系数,我们这里只取x^3的系数就是对应上
上个矩阵行列式的值了。
性质
范德蒙矩阵的性质不多,有两条值得说一下:

范德蒙矩阵与多项式的最小二乘拟合
最后我想谈一谈范德蒙矩阵在多项式的最小二乘拟合中的应用
用一个多项式去拟合若干个点:

假设有n个采样点,拟合次数为k次,那么方差可以表示为:

为求得方差的极小值,对a0,...ak依次求偏导为0。
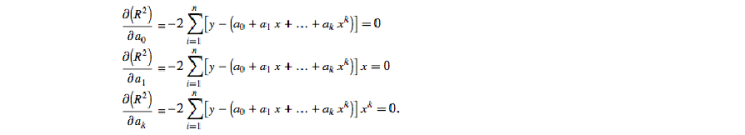
移项
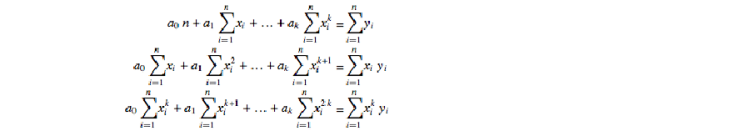
看起来很乱,写成矩阵形式试试:
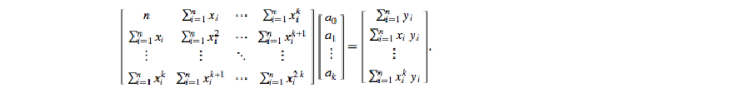
em...这就是个什么矩阵,看起来好复杂滴
哈哈,我们观察变形一下:
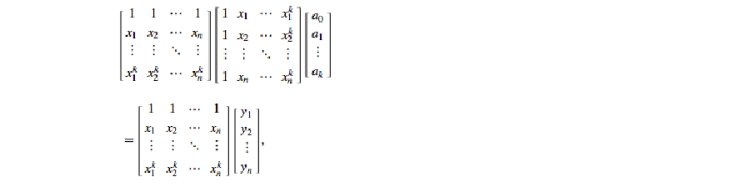
上面的矩阵可以写成范德蒙矩阵相乘的形式哦!

X是竖着的范德蒙矩阵。这样向量a等于:

这里有个很关键的点,范德蒙矩阵不一定是个方阵,即采样点多于拟合多项式的最高次数,不是方阵
就没有逆,但是只要不存在相同的两个采样点,那么
一定是存在逆矩阵的,多项式的系数向量a也可表示出来了。
**这就是基于最小二乘法的多项式拟合原理! **
【1】文档下载
http://www.360doc.com/content/19/0426/19/36378025_831671159.shtml
【2】范德蒙矩阵百度文库
【3】https://blog.csdn.net/weixin_28968629/article/details/113037172