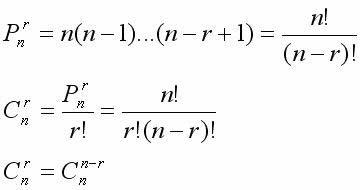阶乘、排列、组合 公式计算
引自:http://wy19880318.blog.163.com/blog/static/3615147220090385546818/
... 

加法原理:做一件事,完成它可以有N类加法,在第一类办法中有M1种不同的方法,在第二类办法中有M2种不同的方法,...,在第N类办法中有MN 种不同的方法。那么完成这件事共有 N=M1+M2+...+MN 种不同的方法。
乘法原理:做一件事,完成它需要分成N个步骤,做第一步有M1种不同的方法,做第二步有M2种不同的方法,...,做第N步有MN种不同的方法,那么完成这件事共有 N=M1×M2×... ×MN 种不同的方法。
排列:从N个不同元素中,任取M(M<=N)个元素,按照一定的顺序排成一列,叫做从N个不同元素中取出M个元素的一个排列。
排列数:从N个不同元素中取出M(M<=N)个元素的所有排列的个数,叫做从N个不同元素中取出M个元素的排列数。记作:Pmn
排列数公式: Pmn =n(n-1)(n-2)...(n-m+1)
全排列:N个不同元素全部取出的一个排列,叫做N个不同元素的一个全排列。
自然数1到N的连乘积,叫做N的阶乘。记作:n! (0!=1)
全排列公式: Pnn =n!
排列数公式还可写成: Pmn = n!/(n-m)!

组合:从N个不同元素中,任取M(M<=N)个元素并成一组,叫做从N个不同元素中取出M个元素的一个组合。
排列 与元素的顺序有关, 组合 与元素的顺序无关。
组合数:从N个不同元素中取出M(M<=N)个元素的所有组合的个数,叫做从N个不同元素中取出M个元素的组合数。记作:Cmn
组合数公式: Cmn = Pmn / Pmm = n(n-1)(n-2)...(n-m+1)/m! = n!/m!/(n-m)!

组合性质1: Cmn = Cn-mn ( C0n =1)
组合性质2: Cmn+1 = Cmn + Cm-1n
over!
公式P是指排列,从N个元素取r个进行排列。排列是分顺序的。
公式C是指组合,从N个元素取r个,不进行组合。组合不分顺序。
如:从1、2、3、4 四个数中选2个数进行排列共
计算:=4*3=12
1、2
1、3
1、4
2、1
2、3
2、4
3、1
3、2
3、4
4、1
4、2
4、3
从1、2、3、4 四个数中选2个数进行组合共
计算:=4*3/2=6
1、2
1、3
1、4
2、3
2、4
3、4