RMQ问题之ST算法

RMQ问题之ST算法

RMQ(Range Minimum/Maximum Query)问题，即区间最值问题。
给你n个数，a₁ , a₂ , a₃ , ... ,a_n，求出区间 [ l , r ]的最大值。

举例：
a={ 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 },求出区间[4 ,8]中的最值。（答案：8 )

这个问题最朴素的想法是用一个循环每次比较大小，但是，当数据范围较大时，这个算法十分低效。这时我们往往使用 ST 算法解决这个问题。虽然线段树和树状数组都能解决，但是ST算法更快。ST算法能做到O(1)时间的查询，而且代码实现更容易。

我们定义 f ( i , j ) 表示从i开始，长度为 2^j 的一段区间中的最大值。

例如：在数列3，2，4，5，6，8，1，2，9，7中，f ( 1 , 0 )表示从第一个数开始长度为20的区间内的最大值，即f ( 1 , 0 ) = 3 , 同理f ( 1 , 1 )=3 , f ( 1 , 2 ) =5, f ( 1 , 3 ) =8。从这里很容易发现，f ( i , 0 ) 等于原数列第i个数的值。

可以通过预处理的递推计算f ( i , j )：

f ( i , j ) = max { f ( i , j-1 )  , f ( i+(1<<j-1) , j - 1 )  }

这个方程与动态规划的思想十分相似，这几乎是ST算法的核心，但是，这个方程是什么意思呢？我们将区间[ i , j ]分成两部分[ i , i+2^j-1 -1 ] 与 [ i+2^j-1 , i+2^j -1] , 这两个区间的长度都为2^j-1，分别求出两个区间最大值，在取较大的那个，就是原区间的最大值。这就是ST算法的动态转移方程。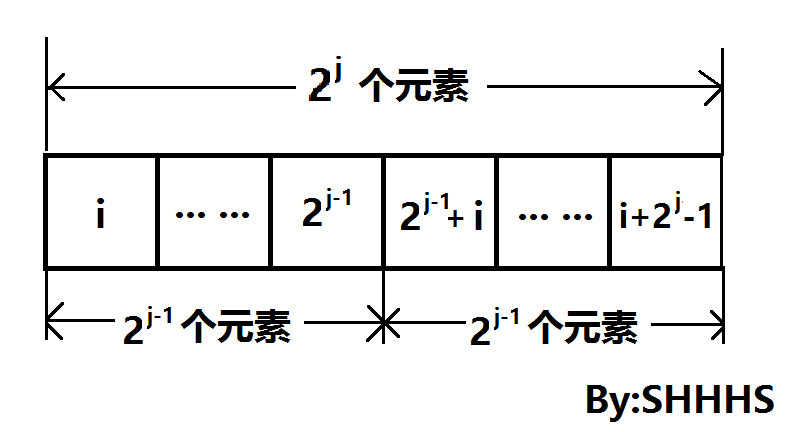

举例：数列a={ 1 ，4 ， 2 ， 3 }求f ( 1 , 2 ) =max { f( 1 , 1 ) , f ( 3 , 1 ) }=max { 4 , 3 } = 4 ;
注：初始状态 f ( i , 0 ) = a [i] ;

预处理：

void Init()//nlogn
{
    log2[1] = 0;
    for(int i = 2; i <= n; i++) log2[i] = log2[i >> 1] + 1; //打log2表
    for(int i = 1; i <= n; i++) f[i][0] = a[i]; //建立初始状态
    for(int j = 1; (1 << j) <= n; j++)
    {
        for(int i = 1; i + (1 << j) - 1 <= n; i++)
        {
            f[i][j] = max( f[i][j - 1] , f[i + (1 << j - 1)][j - 1] ); //动态转移方程
        }
    }
}

查询：

查询区间[a , b ]中最大值，查询的方法比较简单，我们只需要找到一个最大整数 k ，使它满足2k<= b - a +1,例如[ 3 , 11 ] 可以分为 [ 3 , 9 ]
这里我们把待查询的区间分成两个小区间，这两个小区间满足两个条件：（1）这两个小区间要能覆盖整个区间（2）为了利用预处理的结果，要求小区间长度相等。注意两个小区间可能重叠（区间重叠不影响结果）
直接返回 max{ f[a][k] , f[b-(1<<k)+1][k] },于是就求出查询区间中的最大值。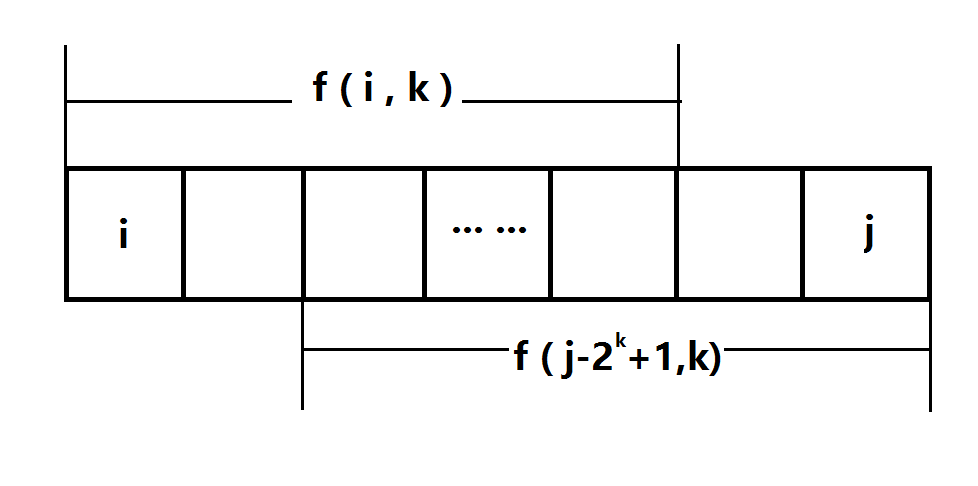

代码如下：

int Query(int a, int b)
{
    int k = log2[b - a + 1];
    return max( f[a][k] , f[b - (1 << k) + 1][k] );
}

主程序：

int main()
{
    int m, u, v;
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        cin >> arr[i];
    }
    Init();
    cin >> m;
    while(m --)
    {
        cin >> u >> v;
        if(u > v) swap(u, v);
        cout << Query(u, v) << endl;
    }
    return 0;
}

综上，ST算法在只有查询的情况下，十分高效，在做了O(nlogn)的预处理后，可以做到O(1)的时间查询。

2016-09-14

(完)