You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Note: Given n will be a positive integer.
Example 1:
Input: 2 Output: 2 Explanation: There are two ways to climb to the top. 1. 1 step + 1 step 2. 2 steps
Example 2:
Input: 3 Output: 3 Explanation: There are three ways to climb to the top. 1. 1 step + 1 step + 1 step 2. 1 step + 2 steps 3. 2 steps + 1 step
题目描述:有 N 阶楼梯,每次可以上一阶或者两阶,求有多少种上楼梯的方法。
分析:这道题是考察斐波那契数列(1,2,3,5,8,13)从第二项开始每个数字都等于前两项的和。
动态规划和递归的区别:递归和动态规划都是将原问题拆成多个子问题然后求解,他们之间最本质的区别是,动态规划保存了子问题的解,避免重复计算。
方法一:递归
时间复杂度:o(n*2) 空间复杂度:o(n)

方法二:动态规划
时间复杂度:o(n) 空间复杂度:o(1)
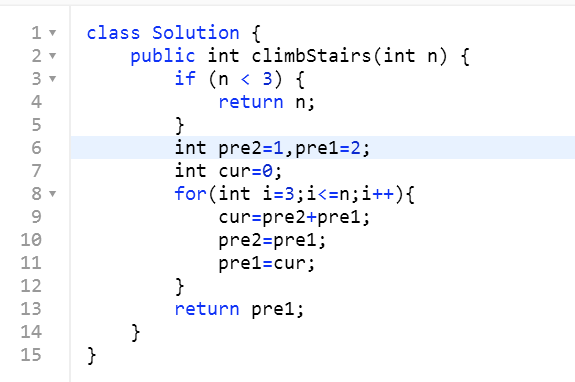
比较两种算法:朴素递归算法之所以效率低是因为它反复求解相同的子问题,动态规划呢,仔细安排了求解顺序,对每个子问题只求解一次,并将结果保存起来。随后如果查找子问题的解只需要找保存的结果,不必重复计算。