全排列的递归和回溯
声明 本文是从p013的排列问题牵扯出的“递归”和“回溯”的自我笔记
本文含大量转载以及整合,参考详见
https://www.jianshu.com/p/a1b3eaf1ed51
https://zhuanlan.zhihu.com/p/92782083
https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-xiang-jie-by-labuladong-2/
https://leetcode-cn.com/u/powcai/
https://baike.baidu.com/item/回溯算法/9258495?fr=aladdin#4
https://blog.csdn.net/yhflyl/article/details/86763197
https://www.cnblogs.com/fanguangdexiaoyuer/p/11224426.html#_label0
课本p013的排列问题描述:

课本提供的递归算法:
package cn.htu.test;
public class Perm {
public static void main(String[] args){
char[] list="ABC".toCharArray();//字符串转化为字符数组
perm(list,0);
}
//如果你debug一下会发现k从头到尾都是0,所以能够让k达到加一的是在参数中加一
private static void perm(char[] list, int k) {
// TODO Auto-generated method stub
//递归结束条件
if (k == list.length) {
for (int i = 0; i < list.length; i++) {
System.out.print(list[i]);
}
System.out.println();
}
else {
for (int i = k; i < list.length; i++) {
{char t=list[k];list[k]=list[i];list[i]=t;}//k和i交换位置
//不要看错了以为k位置和i位置没啥好换的,i并不是一直等于k就只有初始的时候等于k,后面的i都是在k的基础上累加到list.length(即本例的3的)
perm(list, k+1);
{char t=list[k];list[k]=list[i];list[i]=t;}//在交换回来,实际就是回溯
}
}
}
}
上面的是递归算法,但是很难理解,那就先不理解,先看看全排列的回溯算法吧
从全排列看回溯(感谢力扣@labuladong)
在此之前先看一个全排列的树形图(@力扣liweiwei)
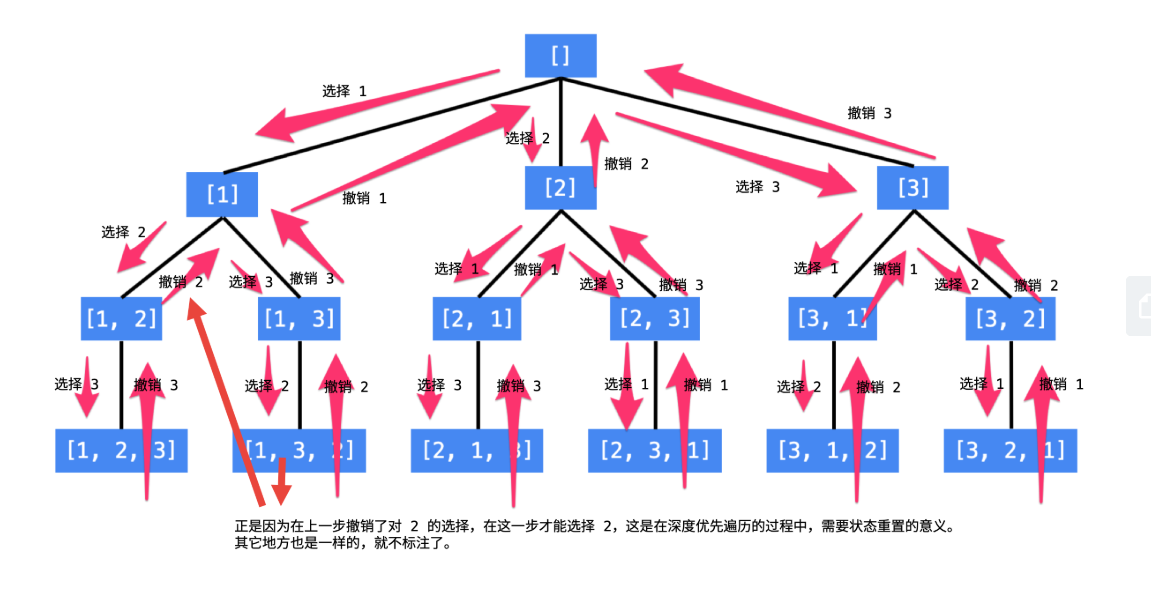
废话不多说,直接上回溯算法框架。解决一个回溯问题,实际上就是一个决策树的遍历过程。你只需要思考 3 个问题:
1、路径:也就是已经做出的选择。
2、选择列表:也就是你当前可以做的选择。
3、结束条件:也就是到达决策树底层,无法再做选择的条件。
如果你不理解这三个词语的解释,没关系,我们后面会用「全排列」和「N 皇后问题」这两个经典的回溯算法问题来帮你理解这些词语是什么意思,现在你先留着印象。
代码方面,回溯算法的框架:
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」,特别简单。
什么叫做选择和撤销选择呢,这个框架的底层原理是什么呢?下面我们就通过「全排列」这个问题来解开之前的疑惑,详细探究一下其中的奥妙!
一、全排列问题
我们在高中的时候就做过排列组合的数学题,我们也知道 n 个不重复的数,全排列共有 n! 个。
PS:为了简单清晰起见,我们这次讨论的全排列问题不包含重复的数字。
那么我们当时是怎么穷举全排列的呢?比方说给三个数 [1,2,3],你肯定不会无规律地乱穷举,一般是这样:
先固定第一位为 1,然后第二位可以是 2,那么第三位只能是 3;然后可以把第二位变成 3,第三位就只能是 2 了;然后就只能变化第一位,变成 2,然后再穷举后两位……
其实这就是回溯算法,我们高中无师自通就会用,或者有的同学直接画出如下这棵回溯树:
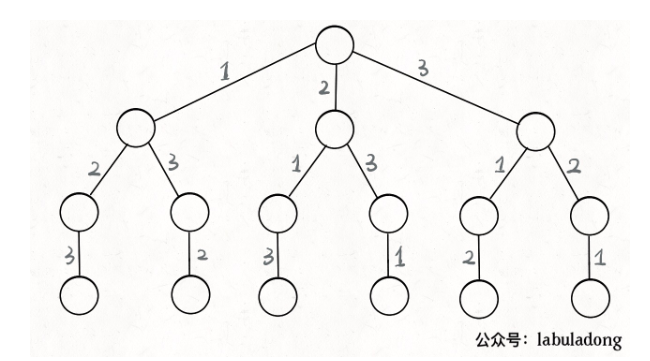
只要从根遍历这棵树,记录路径上的数字,其实就是所有的全排列。我们不妨把这棵树称为回溯算法的「决策树」。
为啥说这是决策树呢,因为你在每个节点上其实都在做决策。比如说你站在下图的红色节点上:

你现在就在做决策,可以选择 1 那条树枝,也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢?因为 2 这个树枝在你身后,这个选择你之前做过了,而全排列是不允许重复使用数字的。
现在可以解答开头的几个名词:[2] 就是「路径」,记录你已经做过的选择;[1,3] 就是「选择列表」,表示你当前可以做出的选择;「结束条件」就是遍历到树的底层,在这里就是选择列表为空的时候。
如果明白了这几个名词,可以把「路径」和「选择」列表作为决策树上每个节点的属性,比如下图列出了几个节点的属性:
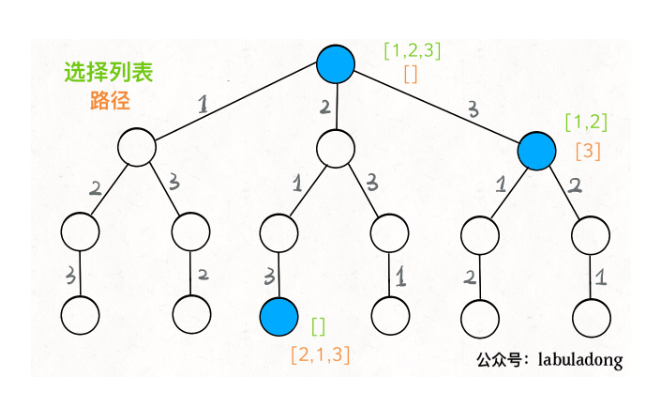
我们定义的 backtrack 函数其实就像一个指针,在这棵树上游走,同时要正确维护每个节点的属性,每当走到树的底层,其「路径」就是一个全排列。
再进一步,如何遍历一棵树?这个应该不难吧。回忆一下之前「学习数据结构的框架思维」写过,各种搜索问题其实都是树的遍历问题,而多叉树的遍历框架就是这样:
void traverse(TreeNode root) {
for (TreeNode child : root.childern)
// 前序遍历需要的操作
traverse(child);
// 后序遍历需要的操作
}
而所谓的前序遍历和后序遍历,他们只是两个很有用的时间点,我给你画张图你就明白了:
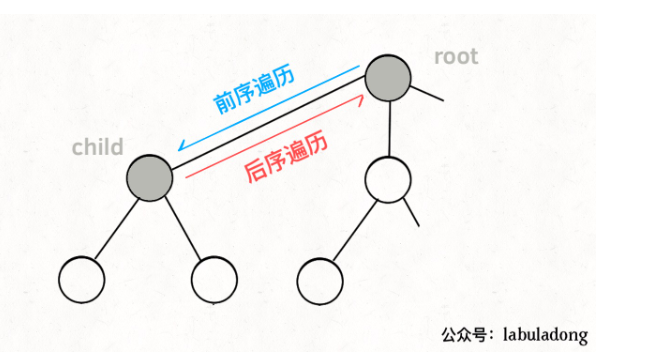
PS:这里真的是颠覆了笔者(S.lee)的一些观念,前序和后序是要看进入和出去结点相对函数来讲的,一个进入一个结点就是进入一个自身函数
前序遍历的代码在进入某一个节点之前的那个时间点执行,后序遍历代码在离开某个节点之后的那个时间点执行。
回想我们刚才说的,「路径」和「选择」是每个节点的属性,函数在树上游走要正确维护节点的属性,那么就要在这两个特殊时间点搞点动作:
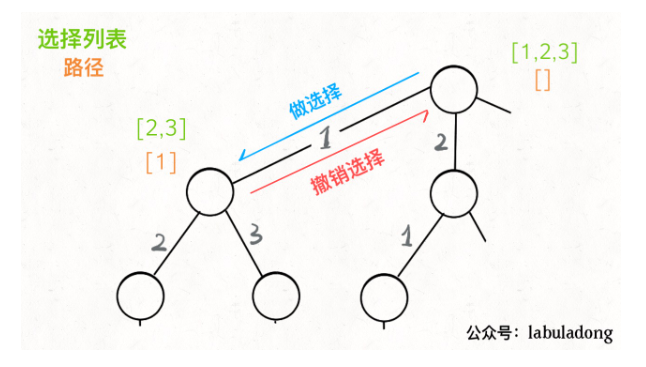
现在,你是否理解了回溯算法的这段核心框架?
for 选择 in 选择列表:
# 做选择
将该选择从选择列表移除
路径.add(选择)
backtrack(路径, 选择列表)
# 撤销选择
路径.remove(选择)
将该选择再加入选择列表
我们只要在递归之前做出选择,在递归之后撤销刚才的选择,就能正确得到每个节点的选择列表和路径。
下面,直接看全排列代码:
package com.htu.test;
import java.util.LinkedList;
import java.util.List;
public class Test {
List<List<Integer>> res = new LinkedList<>();
/* 主函数,输入一组不重复的数字,返回它们的全排列 */
List<List<Integer>> permute(int[] nums) {
// 记录「路径」
LinkedList<Integer> track = new LinkedList<>();
backtrack(nums, track);
return res;
}
// 路径:记录在 track 中
// 选择列表:nums 中不存在于 track 的那些元素
// 结束条件:nums 中的元素全都在 track 中出现
@SuppressWarnings("unchecked")
void backtrack(int[] nums, LinkedList<Integer> track) {
// 触发结束条件
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
// 排除不合法的选择
if (track.contains(nums[i]))
continue;
// 做选择
track.add(nums[i]);
// 进入下一层决策树
backtrack(nums, track);
// 取消选择
track.removeLast();
}
}
}
我们这里稍微做了些变通,没有显式记录「选择列表」,而是通过 nums 和 track 推导出当前的选择列表:
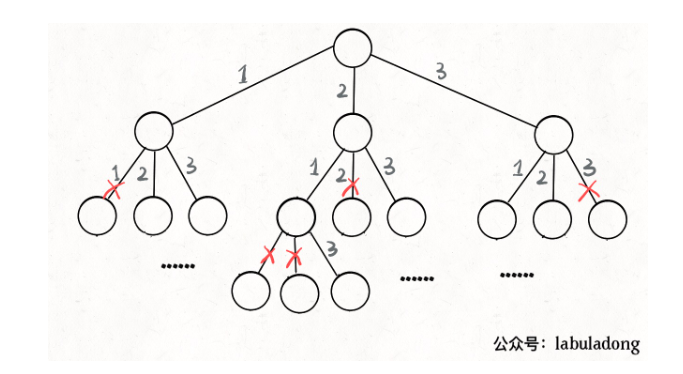
至此,我们就通过全排列问题详解了回溯算法的底层原理。当然,这个算法解决全排列不是很高效,应为对链表使用 contains 方法需要 O(N) 的时间复杂度。有更好的方法通过交换元素达到目的,但是难理解一些,这里就不写了,有兴趣可以自行搜索一下。
但是必须说明的是,不管怎么优化,都符合回溯框架,而且时间复杂度都不可能低于 O(N!),因为穷举整棵决策树是无法避免的。这也是回溯算法的一个特点,不像动态规划存在重叠子问题可以优化,回溯算法就是纯暴力穷举,复杂度一般都很高。
明白了全排列问题,就可以直接套回溯算法框架了,下面简单看看 N 皇后问题。
疫情期间学习效率是真的低,而且在家待时间长了真的不想学习,但是后来发现用博客的方式记录也挺好,没人看,但又有被看到的机会,比离线的记事本更能促进> 学习,hahhahahah,至于N皇后我还没看到,过几天在写代码吧,链接在文字里哦,要记得去吃
再看一小栗子
题目:
给定一个字符串S,通过将字符串S中的每个字母转变大小写,我们可以获得一个新的字符串。返回所有可能得到的字符串集合。
示例:
输入: S = "a1b2"
输出: ["a1b2", "a1B2", "A1b2", "A1B2"]
输入: S = "3z4"
输出: ["3z4", "3Z4"]
输入: S = "12345"
输出: ["12345"]
注意
- S 的长度不超过12。
- S 仅由数字和字母组成。
代码实现
package com.htu.test;
import java.util.LinkedList;
import java.util.List;
public class DiguiHuisu {
/**
*
* @param pre,是一个准备当道res列表里的子串
* @param S,准备处理的模板串
* @param res,最终结果的列表容器
* @param index从第几个元素开始
*/
public static void dfs(String pre, String S, List<String> res, int index) {
System.out.println("该函数被执行一次");
if (index == S.length())//下标index本来是从零开始的,每次在调用自身函数的时候都会+1,最后在自己的身体里自增到等于S.length即3就不能在往下调用自己了,
//所以最后一次它自己调用自己的时候没有完全执行,而是只执行了这个if条件语句,这也是为什么单独的if条件写在前面的原因
res.add(pre);//最后的结果都是在这里结束的,每次都会add一个结果字符串
else {
char ch = S.charAt(index);//ch指向index位置的字符
if (!Character.isLetter(ch))//如果当下字符不是字母的话
dfs(pre + ch, S, res, index + 1);//把数字字符还放到临时的pre里
else {
//下面这段代码按道理说都会顺序执行,但是为什么把ch既变小写又变大写呢,是因为在执行了变小之后
//紧接着又执行自身函数,空
// 小写字符分支
ch = Character.toLowerCase(ch);
dfs(pre + ch, S, res, index + 1);
// 大写字符分支
ch = Character.toUpperCase(ch);
dfs(pre + ch, S, res, index + 1);
}
}
}
public static List<String> letterCasePermutation(String S) {
List<String> res = new LinkedList<>();
dfs("", S, res, 0);
return res;//res是最终返回的结果是个List列表
}
// 测试
public static void main(String[] args) {
String S = "a1b";//输入的串
System.out.println(letterCasePermutation(S));
}
}
相关思想
对于回溯:
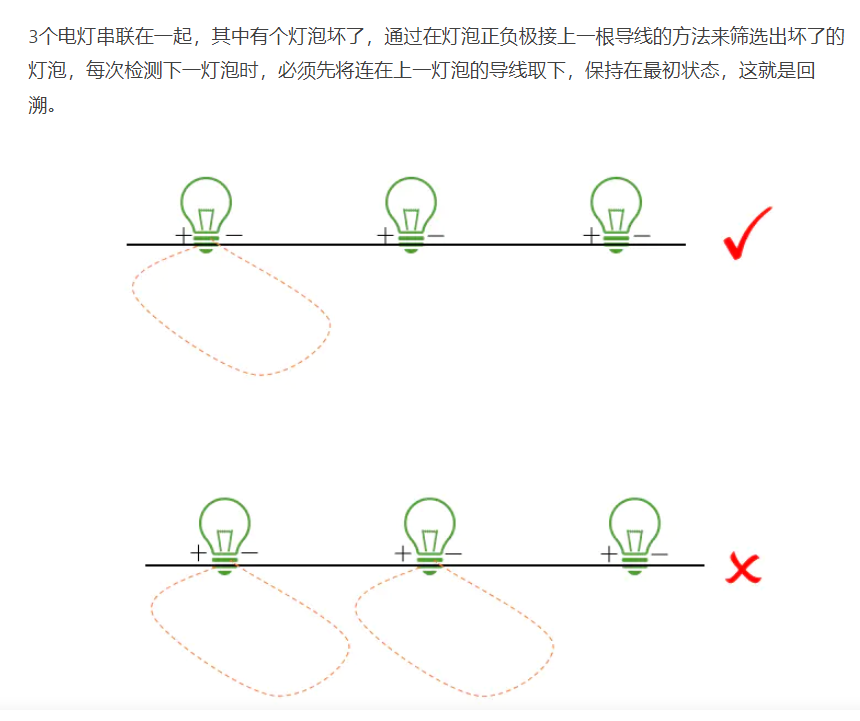
递归与回溯的区别
递归是一种算法结构。递归会出现在子程序中,形式上表现为直接或间接的自己调用自己。典型的例子是阶乘,计算规律为:n!=n×(n−1)!
回溯是一种算法思想,它是用递归实现的。回溯的过程类似于穷举法,但回溯有“剪枝”功能,即自我判断过程。例如有求和问题,给定有 7 个元素的组合 [1, 2, 3, 4, 5, 6, 7],求加和为 7 的子集。累加计算中,选择 1+2+3+4 时,判断得到结果为 10 大于 7,那么后面的 5, 6, 7 就没有必要计算了。这种方法属于搜索过程中的优化,即“剪枝”功能。
用一个比较通俗的说法来解释递归和回溯:
我们在路上走着,前面是一个多岔路口,因为我们并不知道应该走哪条路,所以我们需要尝试。尝试的过程就是一个函数。
我们选择了一个方向,后来发现又有一个多岔路口,这时候又需要进行一次选择。所以我们需要在上一次尝试结果的基础上,再做一次尝试,即在函数内部再调用一次函数,这就是递归的过程。
这样重复了若干次之后,发现这次选择的这条路走不通,这时候我们知道我们上一个路口选错了,所以我们要回到上一个路口重新选择其他路,这就是回溯的思想。
警告:
写递归心得
明白一个函数的作用并相信它能完成这个任务,千万不要试图跳进细节。千万不要跳进这个函数里面企图探究更多细节,否则就会陷入无穷的细节无法自拔,人脑能压几个栈啊。知道套路就行,不要被套路给套了