71: libreoj #10151 区间dp

$des$

https://loj.ac/problem/10151

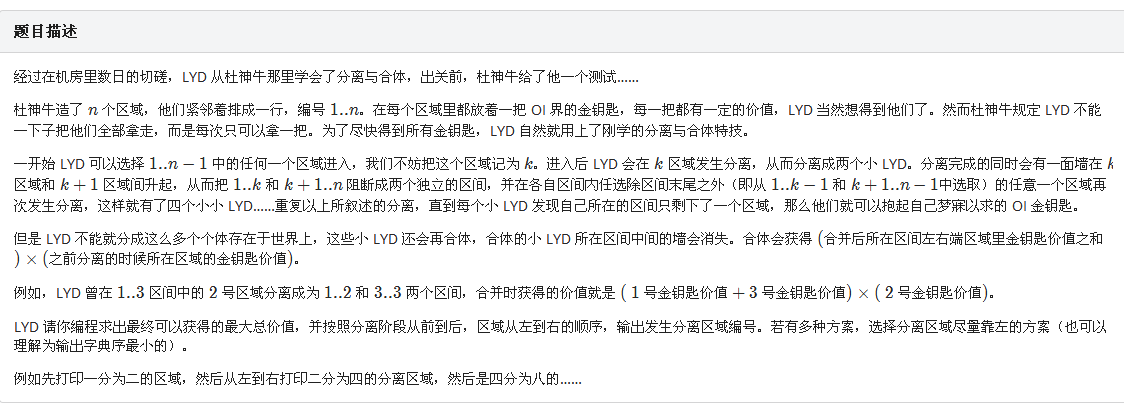
$sol$

区间dp

$f_{i, j}$ 表示区间 $[l, r]$ 合并的最大值

枚举中间点 $k$

$f_{i, j} =max(f_{i, j}, f_{i, k} + f_{k + 1, j} + (w_r + w_{l - 1}) imes w_k)$

对于方案的输出，$g_{i, j}$ 表示区间最优断点

bfs输出

#include <bits/stdc++.h>

const int N = 305;

int f[N][N], g[N][N], w[N], n, sum[N];

int main() {
    std:: cin >> n;
    for(int i = 1; i <= n; i ++) std:: cin >> w[i];
    for(int i = 1; i <= n; i ++) sum[i] = sum[i - 1] + w[i];
    for(int i = 1; i <= n; i ++)
        for(int j = 1; j <= n; j ++)
            f[i][j] = (1 << 29);
    for(int i = 1; i <= n; i ++) f[i][i] = 0;
    for(int len = 2; len <= n; len ++) {
        for(int l = 1; l + len - 1 <= n; l ++) {
            int r = l + len - 1, add = -1;
            for(int k = l; k < r; k ++) {
                int now = f[l][k] + f[k + 1][r] + (w[r] + w[l]) * w[k];
                if(now > add) {
                    add = now, g[l][r] = k;
                }
            }
            f[l][r] = add;
        }
    }
    std:: cout << f[1][n] << "
";
    static int Answer[N], js = 0;
    std:: queue < std:: pair<int, int> > Q;
    Q.push(std:: make_pair(1, n));
    while(!Q.empty()) {
        std:: pair <int, int> tp = Q.front();
        Q.pop();
        Answer[++ js] = g[tp.first][tp.second];
        if(tp.first != g[tp.first][tp.second]) Q.push(std:: make_pair(tp.first, g[tp.first][tp.second]));
        if(tp.second != g[tp.first][tp.second] + 1) Q.push(std:: make_pair(g[tp.first][tp.second] + 1, tp.second));
    }
    for(int i = 1; i <= js; i ++) std:: cout << Answer[i] << " ";
    return 0;
}