矩阵系列

矩阵快速幂的模板

矩阵的知识太多了，这里贴出一部分常用的。

        矩阵的加法运算满足交换律：A + B = B + A^[4]。矩阵的转置和数乘运算对加法满足分配律：

(A + B)^T  A^T + B^T

c(A + B)  cA + cB

       矩阵加法和数乘两种运算使得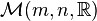成为一个mn维的实数线性空间。而转置和数乘运算满足类似于结合律的规律：

c(A^T)  (cA)^T.

矩阵的乘法满足结合律和对矩阵加法的分配律（左分配律和右分配律）：

• 结合律：   (AB)C  A(BC),
• 左分配律： (A + B)C  AC + BC,
• 右分配律： C(A + B)  CA + CB.

矩阵的乘法与数乘运算之间也满足类似结合律的规律；与转置之间则满足倒置的分配律。

c(AB)  (cA)B  A(cB)

(AB)^T  B^TA^T

矩阵的乘法是相当常用的，利用运算性质找出最优运算顺序可能会大大节省时间。

矩阵乘法不满足交换律

更多的东西详见http://zh.wikipedia.org/wiki/%E7%9F%A9%E9%98%B5#.E7.9F.A9.E9.99.A3.E7.9A.84.E5.9F.BA.E6.9C.AC.E9.81.8B.E7.AE.97

（维基百科）

矩阵的一些题目  

POJ 3070 Fibonacci  详见题解

POJ 3233 Matrix Power Series  详见题解

POJ 3735 Training little cats  详见题解