www.cnblogs.com/shaokele/
luoguP3960 [noip2017]列队##
Time Limit: 2 Sec
Memory Limit: 512 MBDescription###
Sylvia 是一个热爱学习的女♂孩子。
前段时间,Sylvia 参加了学校的军训。众所周知,军训的时候需要站方阵。
Sylvia 所在的方阵中有 (n imes m) 名学生,方阵的行数为 (n) ,列数为 (m) 。
为了便于管理,教官在训练开始时,按照从前到后,从左到右的顺序给方阵中 的学生从 1 到 (n imes m) 编上了号码(参见后面的样例)。即:初始时,第 (i) 行第 (j) 列 的学生的编号是 ((i-1) imes m + j) 。
然而在练习方阵的时候,经常会有学生因为各种各样的事情需要离队。在一天 中,一共发生了 (q) 件这样的离队事件。每一次离队事件可以用数对 ((x,y) (1 le x le n, 1 le y le m)) 描述,表示第 (x) 行第 (y) 列的学生离队。
在有学生离队后,队伍中出现了一个空位。为了队伍的整齐,教官会依次下达 这样的两条指令:
向左看齐。这时第一列保持不动,所有学生向左填补空缺。不难发现在这条 指令之后,空位在第 (x) 行第 (m) 列。
向前看齐。这时第一行保持不动,所有学生向前填补空缺。不难发现在这条 指令之后,空位在第 (n) 行第 (m) 列。
教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后, 下一个学生才能离队。因此在每一个离队的学生要归队时,队伍中有且仅有第 (n) 行 第 (m) 列一个空位,这时这个学生会自然地填补到这个位置。
因为站方阵真的很无聊,所以 Sylvia 想要计算每一次离队事件中,离队的同学 的编号是多少。
注意:每一个同学的编号不会随着离队事件的发生而改变,在发生离队事件后 方阵中同学的编号可能是乱序的。
Input###
输入共 (q+1) 行。
第 1 行包含 3 个用空格分隔的正整数 (n, m, q) ,表示方阵大小是 (n) 行 (m) 列,一共发 生了 (q) 次事件。
接下来 (q) 行按照事件发生顺序描述了 (q) 件事件。每一行是两个整数 (x, y) ,用一个空 格分隔,表示这个离队事件中离队的学生当时排在第 (x) 行第 (y) 列。
Output###
按照事件输入的顺序,每一个事件输出一行一个整数,表示这个离队事件中离队学 生的编号。
Sample Input###
2 2 3
1 1
2 2
1 2
Sample Output###
1
1
4
HINT
【输入输出样例 1 说明】
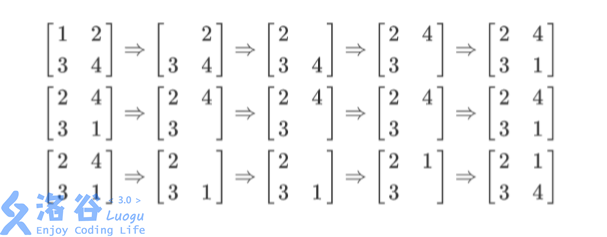
列队的过程如上图所示,每一行描述了一个事件。 在第一个事件中,编号为 (1) 的同学离队,这时空位在第一行第一列。接着所有同学 向左标齐,这时编号为 (2) 的同学向左移动一步,空位移动到第一行第二列。然后所有同 学向上标齐,这时编号为 (4) 的同学向上一步,这时空位移动到第二行第二列。最后编号 为 (1) 的同学返回填补到空位中。
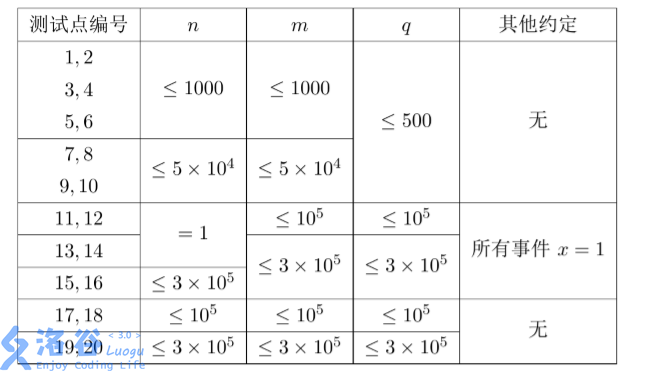
【数据规模与约定】
数据保证每一个事件满足 (1 le x le n,1 le y le m)
题目地址: luoguP3960 [noip2017]列队
题目大意:
一个 (n*m) 的队列,第 (i*j) 行的数编号为 ((i-1)*m+j)
每次取出 (x) 行 (y) 列的数,把它从队列中删去。
把它右边的数都往左移
把最后一列的数都向上移
在把结果插入第 (n) 行 (m) 列
重复上述过程
题解:
容易知道,相邻两行没有影响(除了从最后一列插进来的数)
我们可以对每一行分别做,判断当前取的应该是这一行的第几个数
(可以大于 (m) ,说明是之后从最后一列插进来的)
把最后一列另外做,因为最后一列经常会变
把删除的数插入列的最后一位,维护一下当前行的情况和从最后一列插进来元素的情况
这些都可以用树状数组维护
但如果每行都开结构维护会超空间
所以离线处理
还有开 (long long) 别忘了 =_=
具体看代码
AC代码
#include <cstdio>
#include <vector>
#include <algorithm>
#define ll long long
using namespace std;
const int N=300005;
int n,m,Q,len;
int X[N],Y[N],sol[N];
int T[N+N];
ll Num[N+N];
vector<ll> a[N];
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct node{
int x,y,id;
}A[N];
bool cmp(node a,node b){
if(a.x!=b.x)return a.x<b.x;
return a.id<b.id;
}
void modify(int k,int tot){
for(int i=k;i<=len;i+=i&(-i))
T[i]+=tot;
}
int query(int k){
int res=0;
for(int i=k;i;i-=i&(-i))
res+=T[i];
return res;
}
int search(int tot){ //二分,树状数组维护了前缀和,可以知道所要值的位置
int l=1,r=len,res=-1;
while(l<=r){
int mid=(l+r)>>1;
if(query(mid)>=tot){
res=mid;
r=mid-1;
}else l=mid+1;
}
return res;
}
int main(){
n=read();m=read();Q=read();
len=max(n,m)+Q;
for(int i=1;i<=Q;i++){
A[i].x=X[i]=read();
A[i].y=Y[i]=read();
A[i].id=i;
}
sort(A+1,A+Q+1,cmp); //离线处理,行号为第一关键字,询问的先后为第二关键字
for(int i=1;i<=len;i++)modify(i,1); //当前行的树状数组先都赋1,表示这位有数
//树状数组维护前缀和 ,这里只要维护当前行的树状数组
int pre=1;
for(int i=2;i<=Q+1;i++) //Q+1是保证最后一种行号也会做
if(A[i].x!=A[i-1].x){
for(int j=pre;j<i;j++)
if(A[j].y<m){ //最后一列的另外处理,可以直接从维护列的树状数组里取
sol[A[j].id]=search(A[j].y); //找到这个询问应该在当前行中的位置
modify(sol[A[j].id],-1); //原来的位置删去
//本来应该在最后加1的,因为一开始已经赋了足够长度的1,所以不用了
}
for(int j=pre;j<i;j++) //还原状态
if(A[j].y<m)
modify(sol[A[j].id],1);
pre=i;
}
//这里只要维护最后一列的树状数组,本来要赋值的,原来的1还在就不赋了
for(int i=1;i<=Q;i++){
ll ans;
int k=search(X[i]); //找到现在行的最后一个数是什么
if(k<=n)ans=(ll)k*m;
else ans=Num[k-n]; //ans就是现在行的最后一个数的值
modify(k,-1); //把这个点从列的树状数组中删去
if(Y[i]<m){ //如果现在取的位置不是最后一位,就要更新
a[X[i]].push_back(ans); //把插入的数插入当前行的vector里面
if(sol[i]<m)ans=(ll)(X[i]-1)*m+sol[i]; //如果取的还是原本没动的
else ans=a[X[i]][sol[i]-m]; //如果取的是新插入的,从vector中直接处理
} //这样还可以解决从vector中取出元素再插入vector的情况
Num[i]=ans; //把取出的数插入列的树状数组的最后一位
printf("%lld
",ans);
}
return 0;
}
2018.8.1
经评论区大佬提醒,省去一个 (log)
#include <cstdio>
#include <vector>
#include <algorithm>
#define ll long long
using namespace std;
const int N=300005;
int n,m,Q,len;
int X[N],Y[N],sol[N];
int T[N+N];
ll Num[N+N];
vector<ll> a[N];
inline int read(){
int x=0,f=1;char ch=getchar();
while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
return x*f;
}
struct node{
int x,y,id;
}A[N];
bool cmp(node a,node b){
if(a.x!=b.x)return a.x<b.x;
return a.id<b.id;
}
void modify(int k,int tot){
for(int i=k;i<=len;i+=i&(-i))
T[i]+=tot;
}
int query(int k){
int res=0;
for(int i=k;i;i-=i&(-i))
res+=T[i];
return res;
}
int kth(int k){
int idx=0;
for(int i=20;i>=0;i--){
idx^=(1<<i);
if(idx<=len && k>T[idx])k-=T[idx];
else idx^=(1<<i);
}
return idx+1;
}
int main(){
n=read();m=read();Q=read();
len=max(n,m)+Q;
for(int i=1;i<=Q;i++){
A[i].x=X[i]=read();
A[i].y=Y[i]=read();
A[i].id=i;
}
sort(A+1,A+Q+1,cmp);
for(int i=1;i<=len;i++)modify(i,1);
int pre=1;
for(int i=2;i<=Q+1;i++)
if(A[i].x!=A[i-1].x){
for(int j=pre;j<i;j++)
if(A[j].y<m){
sol[A[j].id]=kth(A[j].y);
modify(sol[A[j].id],-1);
}
for(int j=pre;j<i;j++)
if(A[j].y<m)
modify(sol[A[j].id],1);
pre=i;
}
for(int i=1;i<=Q;i++){
ll ans;
int k=kth(X[i]);
if(k<=n)ans=(ll)k*m;
else ans=Num[k-n];
modify(k,-1);
if(Y[i]<m){
a[X[i]].push_back(ans);
if(sol[i]<m)ans=(ll)(X[i]-1)*m+sol[i];
else ans=a[X[i]][sol[i]-m];
}
Num[i]=ans;
printf("%lld
",ans);
}
return 0;
}