拓扑排序,首先它是一种排序。不过是应用在有向无环图上,将图的结点按照某种规则排成一个线性队列。只不过排序的规则是
对于任意两个结点(u,v),如果他们之间存在边(u->v),那么u必须出现在v之前。
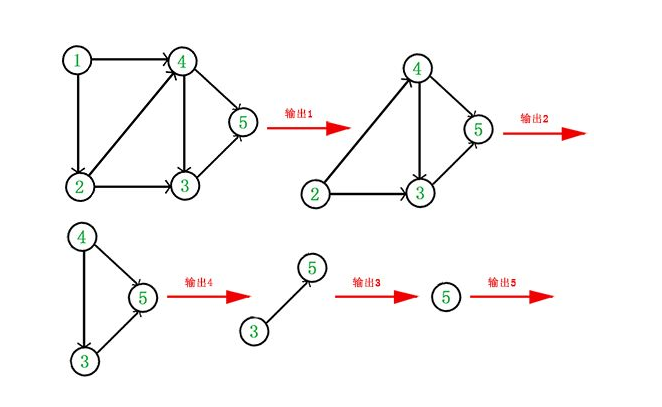
满足拓扑排序的一个有向无环图
那么按照上面的规则我们可以这样实现拓扑排序
1: 找到所有初始入度为0的节点,并将它们放入队列或者栈中,并记录此时入度为0的数目。
2:遍历队列中的结点,对每一个结点,遍历它的直接相连的结点。并将它们入度减一,如果入度为0,将该节点放入队列,更新入度为0的数目(+1)。
3:重复2中操作,直到队列中元素为空,此时比较入度为0的数目和图的总结点数是否相等。如果相等,则可以满足拓扑排序(也就是判断图不存在环),反之不满足。
import java.util.Stack;
/**
* 为了简单起见 使用了邻接矩阵
* sort具体过程如上述所说
*/
public class TopoSort {
public static boolean sort(int[][] matrix, int[] degree) {
Stack<Integer> stack = new Stack();
int count = 0;
for (int i = 0; i < degree.length; i++) {
if (degree[i] == 0) {
stack.push(i);
count++;
}
}
while (!stack.isEmpty()) {
int temp = stack.pop();
for (int i = 0; i < matrix[temp].length; i++) {
if (matrix[temp][i] == 1) {
degree[i]--;
if (degree[i] == 0) {
stack.push(i);
count++;
}
}
}
}
return count == matrix.length;
}
public static void main(String[] args) {
int[][] matrix = {{0, 1, 1, 0, 0},
{0, 0, 1, 1, 0},
{0, 0, 0, 1, 1},
{0, 0, 1, 0, 1},
{0, 0, 0, 0, 0}};
int[] degree = {0, 1, 3, 2, 2};
System.out.println(sort(matrix,degree));
}
}