本篇博客属于理论分析,旨在让我们认识到排序算法的最优性能,是存在一个下界的,也就是如果你想问,存不存在一种排序算法时间复杂度为O(n)呢,这篇文章能很好的回答你:对不起,不存在的,那么这个下界到底是多少呢?我们通过决策树进行分析(决策树实际上反映了信息论中信息的量化,不知道的去百科)。
先给结论:任何只用到比较的算法最坏情况下需要Omega (NlogN)次比较!!!
决策树:用于证明排序算法的下界,是一个二叉树,每个节点是元素之间一组可能的排序,比较的结果是树的边,下图表示将a,b,c排序的算法
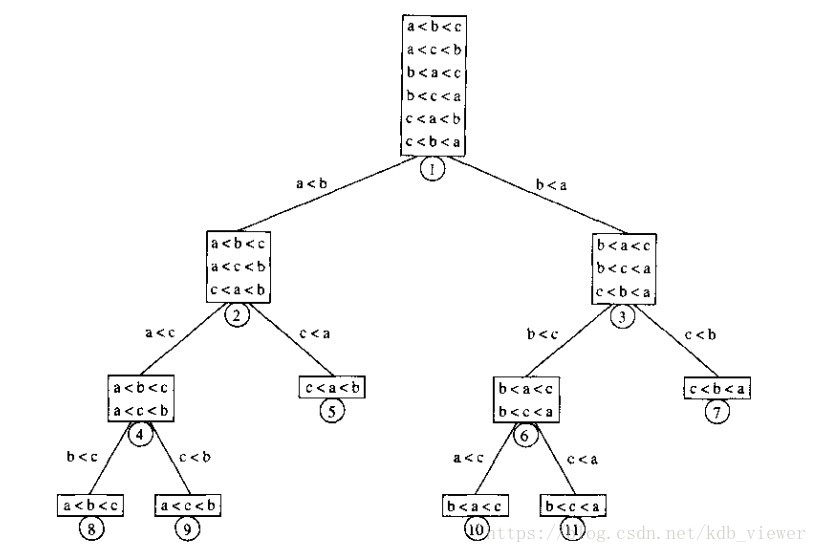
排序算法比较次数等于最深的树叶的深度,平均次数是平均深度
引理1:令T是深度为d的二叉树,那么T最多有2d个树叶
证明:显然
引理2:有L片树叶的二叉树的深度至少是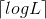
证明:显然
定理1:只用元素之间比较的任何排序算法在最坏情况下至少需要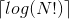 次比较
次比较
证明:对N个元素排序,一定有N!个树叶,因为树叶是每种排序的结果,应用引理2得到结论
定理2:只用元素之间比较的任何排序算法需要进行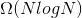 次比较
次比较
证明:

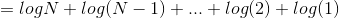
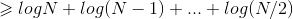
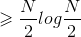


信息论下界:若存在任何P种不同的情况需要区分,问题是yes/no的形式,那么任何算法求解该问题总需要个问题
--------------------
作者:kdb_viewer
来源:CSDN
原文:https://blog.csdn.net/kdb_viewer/article/details/83010155
版权声明:本文为博主原创文章,转载请附上博文链接!