和之前的支持向量机,还有LDA不同,贝叶斯分类器是基于概率模型的分类器;也就是在所有相关概率已知的情况下,贝叶斯决策基于这些概率和误判损失来选择最优的类别标记。
对于贝叶斯分类器,是建立在贝叶斯概率模型上的:
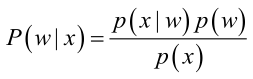
贝叶斯模型是一种典型的”基于结果求原因的模型“,其中:
p(w):为先验概率,表示每种类别分布的概率;
p(x|w):类条件概率(也称似然概率),表示在某种类别的前提下,某事发生的概率。
p(w|x):后验概率,表示某事发生了,并且它属于某一类别的概率,有了这个后验概率,我们就可以对样本进行分类。后验概率越大,说明某事物属于这个类别的可能性越大,我们越有理由把它归到这个类别下。
但是在实际问题中并不都是这样幸运的,我们能获得的数据可能只有有限数目的样本数据,而先验概率p(wi)和类条件概率(各类的总体分布)p(x|w)都是未知的。根据仅有的样本数据进行分类时,一种可行的办法是我们需要先对先验概率和类条件概率进行估计,然后再套用贝叶斯分类器。
先验概率的估计较简单,1、每个样本所属的自然状态都是已知的(有监督学习);2、依靠经验;3、用训练样本中各类出现的频率估计。
类条件概率的估计(非常难),原因包括:概率密度函数包含了一个随机变量的全部信息;样本数据可能不多;特征向量x的维度可能很大等等。总之要直接估计类条件概率的密度函数很难。解决的办法就是,把估计完全未知的概率密度p(x|wi)转化为估计参数。这里就将概率密度估计问题转化为参数估计问题,当然了,对于参数估计问题,概率密度函数的选取很重要,模型正确,在样本区域无穷时,我们会得到较准确的估计值,如果模型都错了,那估计半天的参数,肯定也没啥意义了。
朴素贝叶斯:
假设某个体有n项特征(Feature),分别为F1、F2、...、Fn。现有m个类别(Category),分别为C1、C2、...、Cm。贝叶斯分类器就是计算出概率最大的那个分类,也就是求下面这个算式的最大值:
P(C|F1F2...Fn)= P(F1F2...Fn|C)P(C) / P(F1F2...Fn)
由于 P(F1F2...Fn) 对于所有的类别都是相同的,可以省略,问题就变成了求:
P(F1F2...Fn|C)P(C)
的最大值。
朴素贝叶斯分类器则是更进一步,假设所有特征都彼此独立,因此:
P(F1F2...Fn|C)P(C)= P(F1|C)P(F2|C) ... P(Fn|C)P(C)
关于贝叶斯分类器的描述的网址:
https://blog.csdn.net/fisherming/article/details/79509025,该网址对于贝叶斯分类讲解的非常详细。