一个经典得题目是求平方根(见leetcode第69题)
题目如下,对于某个浮点数x,求其平方根。
方法一:二分法:
这种是最简单的,就是定义一个最小值0和最大值number,把一个数取一个中间值(0+number)/2,然后平方,如果平方大于该数值,就把中间值赋给最大值,否者就把中间值赋给最小值,一直循环,直到取到想要的精度为止。
//二分法 double sqrt1(double x){ double EPSINON = 0.00001; double low = 0.0; double high = x; double mid = (low + high) / 2; while ((high - low) > EPSINON){ if (mid*mid > x){ high = mid; } else{ low = mid; } mid = (high + low) / 2; } return mid; }
方法二:牛顿法
这个也是有迹可循的,求平方根即x^2=n。
令f(x)=x^2-n
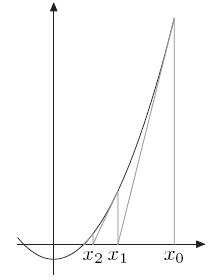
如图所示:
取x0,如果x0不是解,做一个经过(x0,f(x0))这个点的切线,与x轴的交点为x1。
同理,如果x1不是解,做一个经过(x1,f(x1))这个点的切线,与x轴的交点为x2。
以此类推。
以这样的方式得到的xi会无限趋近于f(x)=0的解。
判断xi是否是f(x)=0的解有两种方法:
一是直接计算f(xi)的值判断是否为0,
二是判断前后两个解xi和xi-1是否无限接近。
先采用第一种方法判断
(f(x)-f(xi))/(x-xi)=f’(x),f’(x)是斜率也是f(x)的导函数,即f’(x)=2x。
化简得:f(xi)=f(x)-f’(x)(x-xi),令f(xi)=0得:
(x^2-n)-2x(x-xi)=0
持续化简得:
xx-n-2xx+2xxi=0
2xxi=xx+n
2xi=x+n/x
xi=(x+n/x)/2
这样就得到了一元等式,就可
//牛顿迭代法 double sqrt2(double x) { if (x == 0) return 0; double last = 0.0; double res = 1.0; while (res != last) { last = res; res = (res + x / res) / 2; } return res; }
以进行编程了。