标量：只有大小，没有方向
向量：有大小，有方向
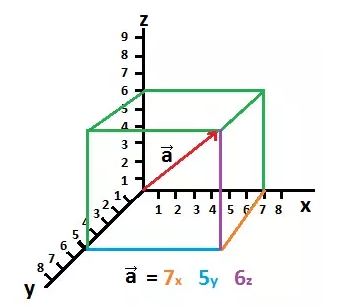
在选定了x,y,z坐标轴之后，我们可以用(7,5,6)表示图中的向量。
那么，什么是张量那？
我们用物理中的一个概念引入张量的概念。
假设我们有一个空心的立方体，立方体中充满着气体，我们通过Force=Stress*Area 可以求得立方体内的气体对立方体内部一个面的压力。
Stress和Area都是向量，并且两者之间的乘法是向量的点乘。
假设Stress用向量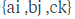
表示，Area用
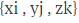表示，经过向量的点乘，我们可以得到Force: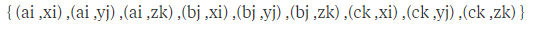
, 它含有九个元素。写成矩阵的形式如下：
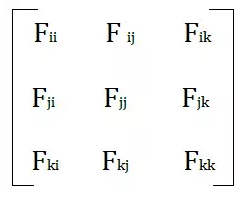
那么这个矩阵跟张量有什么关系那？
我们看矩阵中的第一个元素，
它表示Area和Strss在单位向量(i)方向上的值的乘积。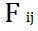
，它表示Stress的单位向量(i)和Area的单位向量(j)方向的数值的乘积。上面这个矩阵就是一个rank-2张量，它表示了单位向量(i)，单位向量(j),单位向量(k)，两两之间的乘积。
也就是说：
标量：有大小，没有方向
向量：有大小，并且只有一个方向
rank-2张量：有大小，并且含有两个方向
rank-0 张量：就是标量
renk-1张量：就是矢量(vector）
。。。
类似的，我们可以得到rank-n张量。
参考：
https://www.quora.com/What-is-a-tensor
https://www.youtube.com/watch?v=f5liqUk0ZTw （推荐科学上网之后，看一下这个老爷爷的视频，讲解的很清楚）