java方式实现堆排序

一、堆排序和堆相关概念描述

　　堆排序是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆的性质：即子结点的值总是小于(或者大于)它的父节点，若子结点的值总是小于它的父节点这堆叫大顶堆，子结点的值总是大于它的父节点这种堆叫小顶堆。若二叉树的深度为h，除第 h 层外，其它各层 (1~h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。如果完全二叉树有n个节点，那么有n/2(n为偶数)个叶子节点或(n+1)/2（n为奇数）个叶子节点。

二、基本思想

　　先将数组array[0，...，n-1]构造成一个堆，即将array[0，...，n-1]看成是一颗完全二叉树的顺序存储结构。然后将堆调整为大顶堆（顺序排序），具体步骤如下，先找到堆的非叶子节点array[i](当n为偶数时(n-1)/2<=i<=n-1,当n为奇数时(n-2)/2<=i<=n-1),再找到这个非叶子节点的左右孩子节点（array[2i+1],array[2i+2])，将非叶子节点的值与左右孩子节点的值比较，如果非叶子节点的值小于左右孩子节点值的最大值，把最大孩子节点的最大值赋给非叶子节点，再继续找孩子节点的孩子节点，重复上述比较操作，直到找不到孩子节点为直，当所有非叶子节点重复上述操作完成时，那么这个堆就是大顶堆了。然后将堆顶元素与堆尾元素交换，将堆尾元素移除，将剩余元素组成的堆继续重复调整为大堆，交换堆顶堆尾元素，移除堆尾元素，直到剩余元素组成的堆只有一个元素为止。

三、实现步骤

1. 构建初始堆，将待排序列构成一个大顶堆(或者小顶堆)，升序大顶堆，降序小顶堆；
2. 将堆顶元素与堆尾元素交换，移除堆尾元素。
3. 重新构建大顶堆。
4. 重复2~3，直到待排序列中只剩下一个元素(堆顶元素)。

四、案例分析

 　　以数组{6,5,3,1,8,7}为例如下图：

　　

 

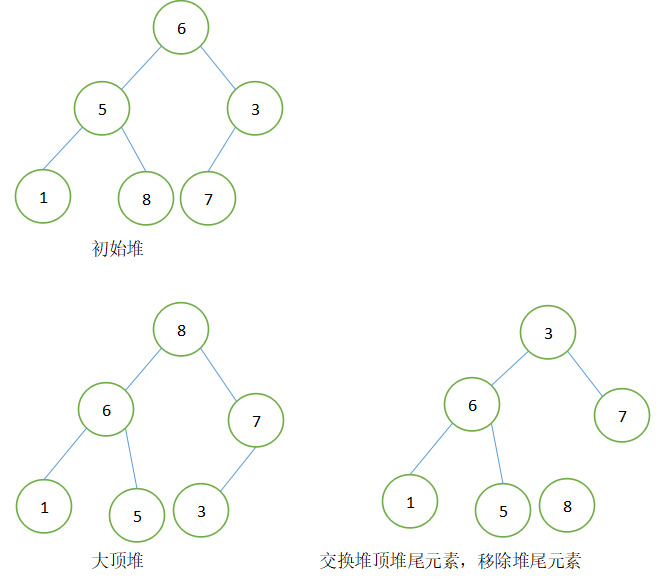
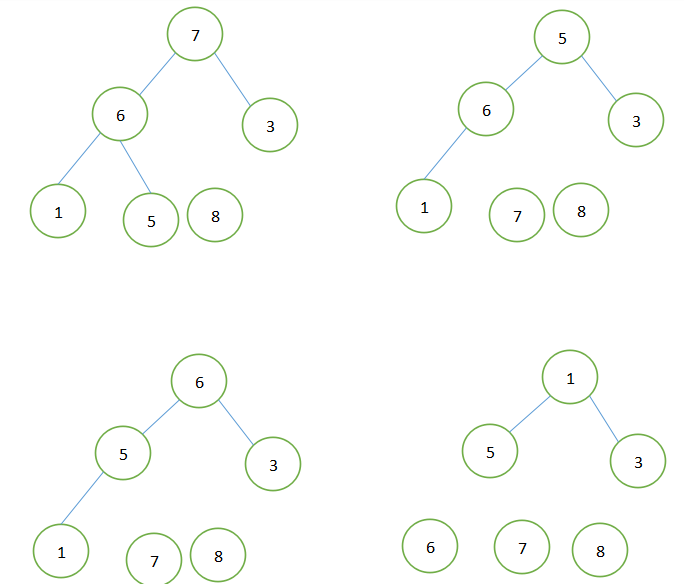
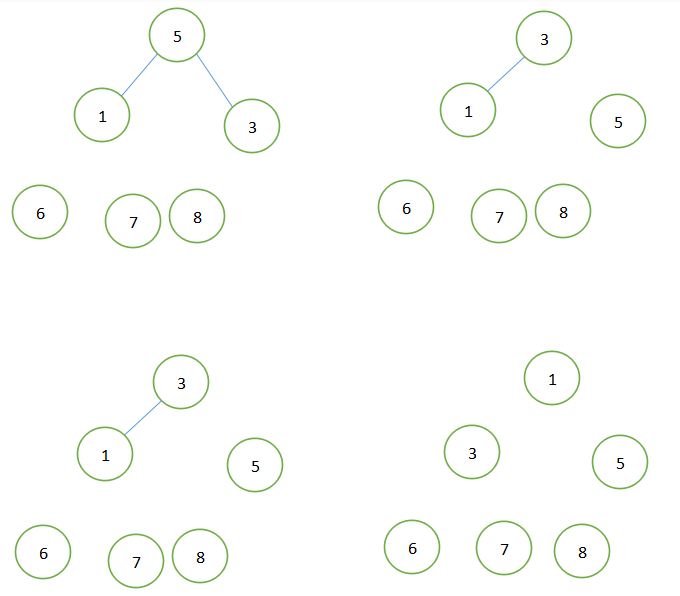
五、代码实现

public class JavaSort {
    public static void main(String[] args) {
        int a [] =new int []{6,5,3,1,8,7};
        System.out.println("排序前的数组："+Arrays.toString(a));
        heapSort(a);
        System.out.println("排序后的数组："+Arrays.toString(a));
    }
    

    

        /**
         * 
         * @param ary 待排序列
         */
        private static void heapSort(int[] ary) {
            int len=ary.length;
            if (len<=0) {
                System.out.println("数组长度不能小于等于0");
            } else if (len==1) {
            }  else {
                int firstIndex=len-1;
                if(len%2==0) {
                    firstIndex=len-2;//第一个非叶子节点位置,如果数组长度为偶数，非叶子节点为length-2/2,否则叶子长度为length-1/2.
                } 
                 for (int i = firstIndex / 2; i >= 0; i--) {
                     //从第一个非叶子结点从下至上，从右至左调整结构,把堆调整为大顶堆。
                     adjustHeap(ary, i, ary.length);
                 }
                System.out.println("第一次构造的大顶堆"+Arrays.toString(ary));

                 //调整堆结构+交换堆顶元素与末尾元素
                 for (int i = ary.length - 1; i > 0; i--) {
                     //将堆顶元素与末尾元素进行交换
                     int temp = ary[i];
                     ary[i] = ary[0];
                     ary[0] = temp;
                     //将数组长度-1，移除堆尾元素，将堆顶元素进行调整，就可以将堆调整为大顶堆
                     System.out.println("要移除的堆尾元素："+ary[i]);
                     System.out.println("移除堆尾元素后，堆为"+Arrays.toString(Arrays.copyOfRange(ary, 0, i)));
                     adjustHeap(ary, 0, i);
                     System.out.println("移除堆尾元素后，大顶堆堆为"+Arrays.toString(Arrays.copyOfRange(ary, 0, i)));

                 }
                 
            }
            
            
           
        }

        /**
         * 调整完全二叉树的非叶子节点，使得它们的节点值大于左右孩子节点的值，左右孩子重复上述操作，直到找不到孩子节点。
         * @param ary 要调整的数组
         * @param parent 要调整的节点
         * @param length 要调整的数组长度
         */
        private static void adjustHeap(int[] ary, int parent, int length) {
            //将temp作为父节点
            int temp = ary[parent];
            //左孩子
            int lChild = 2 * parent + 1;

            while (lChild < length) {
                //右孩子
                int rChild = lChild + 1;
                // 如果有右孩子结点，并且右孩子结点的值大于左孩子结点，则选取右孩子结点
                if (rChild < length && ary[lChild] < ary[rChild]) {
                    lChild++;
                }

                // 如果父结点的值已经大于孩子结点的值，则直接结束
                if (temp >= ary[lChild]) {
                    break;
                }

                // 把孩子结点的值赋给父结点
                ary[parent] = ary[lChild];

                //选取孩子结点的左孩子结点,继续向下找
                parent = lChild;
                lChild = 2 * lChild + 1;
            }
            ary[parent] = temp;
            
        }
    
}

五、运行结果

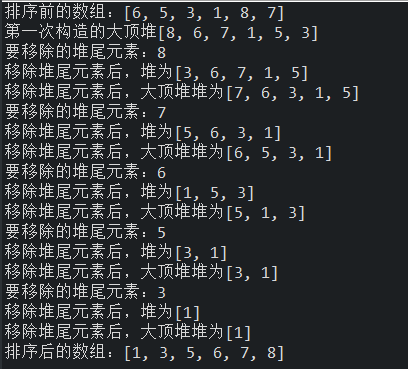
六、运行结果

　　空间复杂度:o(1)。

　　时间复杂度:建堆：o(n)，每次调整o(log n)，故最好、最坏、平均情况下：o(n*logn)。

　　稳定性：不稳定。