.8 AVL树

平衡二叉树（Balanced Binary Tree）是二叉查找树的一个进化体，也是第一个引入平衡概念的二叉树。1962年，G.M. Adelson-Velsky 和 E.M. Landis发明了这棵树，所以它又叫AVL树。平衡二叉树要求对于每一个节点来说，它的左右子树的高度之差不能超过1，如果插入或者删除一个节点使得高度之差大于1，就要进行节点之间的旋转，将二叉树重新维持在一个平衡状态。这个方案很好的解决了二叉查找树退化成链表的问题，把插入，查找，删除的时间复杂度最好情况和最坏情况都维持在O(logN)。但是频繁旋转会使插入和删除牺牲掉O(logN)左右的时间，不过相对二叉查找树来说，时间上稳定了很多。

（1）左左  （2）左右  （3）右左  （4）右右

     

       对于“左左”和“右右”的情况，只要进行一次单旋转就可以使其恢复平衡。如下图：

       

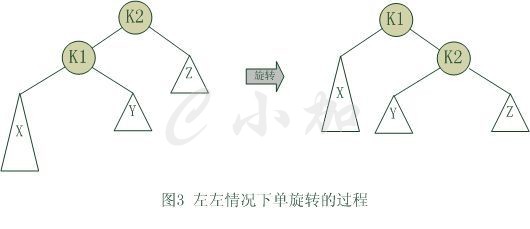
相应的给出代码：

//左左
TreeNode *SingleRotateLeft(TreeNode *t2)
{
    TreeNode *t1;
    t1 = t2->left;
        t2->left = t1->right;
    t1->right = t2;

    t2->height = max(getHeight(t2->left),getHeight(t2->right)) + 1;
    t1->height = max(getHeight(t1->left),getHeight(t1->right)) + 1;
    return t1;
}

//右右
 TreeNode *SingleRotateRight(TreeNode *t2)
 {
     TreeNode *t1;
     t1 = t2->right;
     t2->right = t1->left;
     t1->left = t2;

     t2->height = max(getHeight(t2->left),getHeight(t2->right)) + 1;
     t1->height = max(getHeight(t1->left),getHeight(t1->right)) + 1;
     return t1;
 }

对于“左右”和“右左”则要进行一次双旋转，如下图：

相应的代码：

//左右
TreeNode * DoubleRotateLR(TreeNode *t3)
{
 t3->left = SingleRotateRight(t3->left);
 return SingleRotateLeft(t3);
}

//右左
TreeNode * DoubleRotateRL(TreeNode *t3)
{
 t3->right = SingleRotateLeft(t3->right);
 return SingleRotateRight(t3);
}

avl.h

#ifndef AVL_H
#define AVL_H

typedef struct avlNode
{
    int k ;
    struct avlNode * lchild ,* rchild ;
    int h ;
}avlnode , * avltree ;

avltree insert( avltree *T , int k ) ;
void del(avltree * T) ;
avltree search( avltree T , int k ) ;
avltree print( avltree T ) ;
void in_order_traverse( avltree T ) ;
#endif // AVL_H

utl.h

#ifndef UTL_H
#define UTL_H
#include<stdio.h>
#include<stdlib.h>

inline void * xalloc(int size)
{
    void *p ;
    p = malloc(size) ;
    if(! p){
        fprintf(stderr , "malloc error
");
        exit(EXIT_FAILURE) ;
    }

    return p ;
}

#define xfree(p) free(p)
#endif // UTL_H

avl.c

#include"avl.h"
#include"utl.h"

int max(int a , int b ) ;
int height(avltree T) ;

avltree singleRotate_l(avltree T ) ;
avltree singleRotate_r(avltree T) ;
avltree doubleRotate_lr(avltree T) ;
avltree doubleRotate_rl(avltree T) ;
//void in_order_traverse(avltree T) ;

void pre_order_traverse( avltree T )
{
    if( T ){
        printf("%d " , T->k ) ;
        pre_order_traverse( T->lchild ) ;
        pre_order_traverse( T->rchild ) ;
    }
}

void in_order_traverse( avltree T)
{
    if(T) {
        in_order_traverse( T->lchild ) ;
        printf("%d " , T->k ) ;
        in_order_traverse( T->rchild ) ;
    }
}

avltree insert(avltree *T , int k)
{
    if(! (*T) ) {
        (*T) = (avltree)xalloc(sizeof(avlnode)) ;
        (*T)->k = k ;
        (*T)->lchild = (*T)->rchild = NULL ;
        (*T)->h = 0 ;
    }
    else if( k < (*T)->k ) {
            //插入左子树
        (*T)->lchild = insert(&(*T)->lchild , k) ;

        if( height( (*T)->lchild) - height((*T)->rchild) == 2) {  //如果树不平衡 则旋转
            if( k < (*T)->lchild->k ) {                 //单旋
                (*T) = singleRotate_l( (*T) ) ;
            }
            else {                                                    //双旋转
                (*T) = doubleRotate_lr( (*T) ) ;
            }
        }

    }

    else if( k > (*T)->k ) {   // 插入右子树
        (*T)->rchild = insert( &(*T)->rchild , k ) ;

        if( height( (*T)->rchild) - height((*T)->lchild ) == 2) {
        if( k > (*T)->rchild->k ) {
            (*T) = singleRotate_r( (*T) ) ;
        }
        else {
            (*T) = doubleRotate_rl( (*T) ) ;
        }
    }
    }

    (*T)->h = max( height( (*T)->lchild) , height( (*T)->rchild) ) + 1 ;
    return (*T) ;
}


avltree singleRotate_l( avltree T )
{
    avltree T1  = T->lchild ;
    T->lchild = T1->rchild ;
    T1->rchild = T ;

    T->h = max( height( T->lchild ) , height( T->rchild ) ) + 1 ;
    T1->h = max(height( T1->lchild ) , height( T1->rchild) ) + 1 ;
    return T1 ;
}

avltree singleRotate_r( avltree T)
{
    avltree T1  = T->rchild ;
    T->rchild = T1->lchild ;
    T1->lchild = T ;

    T->h = max( height( T->lchild ) , height( T->rchild ) ) +1 ;
    T1->h = max( height( T1->lchild ) , height( T1->rchild ) ) +1 ;
    return T1 ;
}

avltree doubleRotate_lr( avltree T )
{
    T->lchild = singleRotate_r( T->lchild ) ;
    return singleRotate_l( T ) ;
}

avltree doubleRotate_rl( avltree T )
{
    T->rchild = singleRotate_l( T->rchild ) ;
    return singleRotate_r( T ) ;
}

int max( int a , int b )
{
    return a>b?a:b ;
}

int height( avltree T )
{
    if(! T ) return -1 ;
    return T->h ;
}



int main()
{
    int i ;
    avltree T = NULL ;
    for(i = 0 ; i < 7 ; i++) {
        insert( &T , i ) ;
    }
    in_order_traverse( T ) ;
    printf("
") ;
    pre_order_traverse( T ) ;
    return 0 ;
}

参考：http://blog.csdn.net/wypblog/article/details/8119616

http://blog.csdn.net/realxuejin/article/details/12872035

http://www.cppblog.com/cxiaojia/archive/2013/07/22/187776.html