围豆豆
题目描述
是不是平时在手机里玩吃豆豆游戏玩腻了呢?最近MOKIA手机上推出了一种新的围豆豆游戏,大家一起来试一试吧。
游戏的规则非常简单,在一个N×M的矩阵方格内分布着D颗豆子,每颗豆有不同的分值Vi。游戏者可以选择任意一个方格作为起始格,每次移动可以随意的走到相邻的四个格子,直到最终又回到起始格。最终游戏者的得分为所有被路径围住的豆豆的分值总和减去游戏者移动的步数。矩阵中某些格子内设有障碍物,任何时刻游戏者不能进入包含障碍物或豆子的格子。游戏者可能的最低得分为0,即什么都不做。
注意路径包围的概念,即某一颗豆在路径所形成的多边形(可能是含自交的复杂多边形)的内部。下面有两个例子:
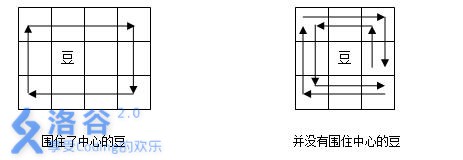
第一个例子中,豆在路径围成的矩形内部,所以豆被围住了。第二个例子中,虽然路径经过了豆的周围的8个格子,但是路径形成的多边形内部并不包含豆,所以没有围住豆子。
布布最近迷上了这款游戏,但是怎么玩都拿不了高分。聪明的你决定写一个程序来帮助他顺利通关。
Input
第一行两个整数N和M,为矩阵的边长。 第二行一个整数D,为豆子的总个数。 第三行包含D个整数V1到VD,分别为每颗豆子的分值。 接着N行有一个N×M的字符矩阵来描述游戏矩阵状态,0表示空格,#表示障碍物。而数字1到9分别表示对应编号的豆子。
Output
仅包含一个整数,为最高可能获得的分值。
Sample Input
3 8
3
30 -100 30
00000000
010203#0
00000000
Sample Output
38
Hint
50%的数据满足\(1≤D≤3\)。
100%的数据满足\(1≤D≤9,1≤N, M≤10,-10000≤V_i≤10000\)。
题解
解题思路
这道题看起来挺难的,就是挺难
但看到数据范围\(1≤D≤9,1≤N, M≤10,-10000≤V_i≤10000\)
挺小的
考虑暴力状态压缩DP
用一串二进制数代表每个豆子的包含情况
例如\(11010\)表示包含2,4,5号豆子
还有就是判断一个点是否在多边形里
从这个点作任意一条射线,如果与多边形交点个数为奇数,则在多边形内,否则不在
如果这条射线正好过边,那就没法求交点个数,所以我们只统计垂直过这条射线的(只针对于这道题)
在看一下下面这个例子
0******0
0*0000*0
0*1****0
0***0000
就像这样,1右面过4个点,但1实际上是在这个多边形内
统计的时候就统一统计这条边下面的点
代码
#include <cstdio>
#include <queue>
#include <cstring>
using namespace std;
const int N = 12;
int n, m, d, M, a[N], sum[1<<N], f[N][N][1<<N], v[N][N][1<<N], ans;
int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0}, fx[N], fy[N], cnt;
char c[N][N];
struct node {
int x, y, s;
node(int a, int b, int c) {
x = a; y = b; s = c;
}
};
queue<node> q;
void bfs(int x, int y) {
memset(f, 0x3f, sizeof(f));
memset(v, 0, sizeof(v));
q.push(node(x, y, 0));
f[x][y][0] = 0;
while (!q.empty()) {
node b = q.front(); q.pop();
v[b.x][b.y][b.s] = 1;
for(int i = 0; i < 4; i++) {
int xx = b.x + dx[i], yy = b.y + dy[i], s = b.s;
if (xx < 1 || yy < 1 || xx > n || yy > m || c[xx][yy] != '0') continue;
if (i >= 2)
for(int j = 1; j <= d; j++)
if (fx[j] == min(b.x, xx) && yy > fy[j])
s ^= 1 << (j - 1);
if (!v[xx][yy][s] && f[xx][yy][s] > f[b.x][b.y][b.s]) {
v[xx][yy][s] = 1;
f[xx][yy][s] = f[b.x][b.y][b.s] + 1;
q.push(node(xx, yy, s));
}
}
}
for(int i = 0; i < M; i++)
ans = max(ans, sum[i] - f[x][y][i]);
}
int main() {
scanf("%d%d%d", &n, &m, &d);
for(int i = 1; i <= d; i++)
scanf("%d", &a[i]);
M = 1 << d;
for(int i = 0; i < M; i++)
for(int j = 1; j <= d; j++)
if (i & (1 << (j - 1)))
sum[i] += a[j];
for(int i = 1; i <= n; i++)
scanf("%s", c[i]+1);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
if (c[i][j] > '0' && c[i][j] <= '9')
fx[c[i][j]-'0'] = i, fy[c[i][j]-'0'] = j;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
if (c[i][j] == '0') bfs(i, j);
printf("%d", ans);
return 0;
}