联赛前第八阶段总结

这阶段考试除了最后一场发挥都挺好的，就是最后一场挂了160分，
最接近前三的一次，和第3差140分，昨天一晚上都没心情改题
上个阶段也是，和第12差70分，倒数第二场挂了80分
可能是到了后期心态就会出现点小问题
但我感觉其实考试的时候状态还是不错的，该想到的也都想到了，就是细节挂掉了
距CSP还有6天，调整好状态，争取不挂分

联赛模拟测试27

阶段排名 5

挂了160

A 物理课

• 根据题目下面的提示我丰富的物理知识，显然会有这么一个式子

[sum_{i}2frac{vsin heta}{g}vcos heta (d^2)^i=sum_{i}frac{v^2sin2 heta}{g}(d^2)^i ]

• 显然用等比数列求和公式可以解决

[sum_{i}frac{v^2sin2 heta}{g}(d^2)^i=frac{frac{v^2sin2 heta}{g}(1-(d^2)^n)}{1-d^2} ]

• 考虑猫跳到什么时候停止，肯定是((d^2)^n)无限接近于0的时候停止，就把这项看成0，最后的式子就是

[ans=frac{v^2sin2 heta}{g(1-d^2)} ]

• 这道题最可恶的地方在于出题人卡精度，pi得精确到小数点后14位，少一位都是0分，所以还是写成acos(-1)吧

• 话说我之前连acos是啥也不知道，acos就是从cos的反函数

Show Code

#include <cmath>
#include <cstdio>

const double pi = acos(-1);
double k, v, d, g, s;
int T;

int main() {
    freopen("physics.in", "r", stdin);
    freopen("physics.out", "w", stdout);
    scanf("%d
", &T);
    while (T--) {
        scanf("%lf%lf%lf%lf", &k, &v, &d, &g);
        printf("%.5lf
", sin(pi * k / 90) / g * v * v / (1 - d * d));
    }
    return 0;
}

B 数学课

• 找规律，这我也不知道该咋说，注意细节就好，考场上有个地方算2的num次方用的左移，挂了60分，不想说了

• 一个快速幂从20分到80分，一个lucas从80到100

Show Code

#include <cstdio>

typedef long long ll;
const int N = 1e7 + 100, M = 1e7 + 19;

ll read(ll x = 0, int f = 1, char c = getchar()) {
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-') f = -1;
    for (; c >= '0' &&  c <= '9'; c = getchar())
        x = x * 10 + c - '0';
    return x * f;
}

ll n, q, sum, tot, mul = 1;
int fac[N], fai[N];

int Pow(int a, ll k, int ans = 1) {
    for (; k; k >>= 1, a = 1LL * a * a % M)
        if (k & 1) ans = 1LL * ans * a % M;
    return ans;
}

int C(int n, int m) {
    if (n < 0 || m < 0 || n < m) return 0;
    return 1LL * fac[n] * fai[m] % M * fai[n-m] % M; 
}

int Lucas(ll n, ll m) {
    if (!m) return 1;
    return 1LL * C(n % M, m % M) * Lucas(n / M, m / M) % M;
}

int main() {
    freopen("math.in", "r", stdin);
    freopen("math.out", "w", stdout);
    n = read(); q = read();
    for (ll x = n, i = 1; x >= 1; x >>= 1, ++i) {
        ll num = (x + 1 >> 1) - (x / 2 + 1 >> 1);
        sum += i / 2 * num;
        if (i & 1) tot += num;
        else mul = mul * Pow(2, num) % M;
    }
    fac[0] = 1;
    int mx = n < M - 1 ? n : M - 1;
    for (int i = 1; i <= mx; ++i)
        fac[i] = 1LL * fac[i-1] * i % M;
    fai[mx] = Pow(fac[mx], M - 2);
    for (int i = mx; i >= 1; --i)
        fai[i-1] = 1LL * fai[i] * i % M;
    while (q--) printf("%lld
", mul * Lucas(tot, read() - sum) % M);
    return 0;
}

C 地理课

• 考场上并查集+暴搜拿了50分暴力，看他们有暴力直接A的，跑的比真解还快

• 一条边只存在一段时间，就线段树分治一下，拍到线段树上，遍历每个节点，加上这个节点记录的边，回溯时删掉，其实就是维护一个可撤销并查集

• 可撤销并查集就是只要不路径压缩就行，我是用的启发式合并，合并的时候记录下来，注意删边的时候要倒着删

Show Code

#include <cstdio>
#include <vector>
#define re register
#define ls (rt << 1)
#define rs (rt << 1 | 1)

const int N = 1e5 + 5, M = 1e9 + 7, M2 = 1e5 + 3;

int read(re int x = 0, re int f = 1, re char c = getchar()) {
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-') f = -1;
    for (; c >='0' && c <='9'; c = getchar())
        x = x * 10 + c - '0';
    return x * f;
}

struct Hash {
    int next, x, y, id;
}h[N];
int head[N], hac;
int n, m, r[N], id[N], f[N], siz[N], inv[N], ans[N];
std::vector<int> t[N<<2];

void Add(int x, int y, int id) {
    int ha = (1LL * x * N + y) % M2;
    h[++hac] = (Hash) {head[ha], x, y, id};
    head[ha] = hac;
}

int Find(int x, int y) {
    int ha = (1LL * x * N + y) % M2;
    for (int i = head[ha]; i; i = h[i].next)
        if (h[i].x == x && h[i].y == y) return i;
    return 0;
}

void Change(int rt, int l, int r, int x, int y) {
    if (x <= l && r <= y) 
        return t[rt].push_back(id[x]), void();
    int mid = l + r >> 1;
    if (x <= mid) Change(ls, l, mid, x, y);
    if (y > mid) Change(rs, mid + 1, r, x, y);
}

int Find(int x) {
    return x == f[x] ? x : Find(f[x]);
}

void Dfs(int rt, int l, int r, int s) {
    std::vector<int> fx, fy;
    for (int i = 0; i < t[rt].size(); ++i) {
        int x = Find(h[t[rt][i]].x);
        int y = Find(h[t[rt][i]].y);
        if (x == y) continue;
        if (siz[x] > siz[y]) std::swap(x, y);
        fx.push_back(x); fy.push_back(y);
        s = 1LL * s * inv[siz[x]] % M * inv[siz[y]] % M;
        f[x] = y;
        siz[y] += siz[x];
        s = 1LL * s * siz[y] % M;
    }
    if (l == r) ans[l] = s;
    else {
        int mid = l + r >> 1;
        Dfs(ls, l, mid, s);
        Dfs(rs, mid + 1, r, s);
    }
    for (int i = fx.size() - 1; i >= 0; --i) {
        siz[fy[i]] -= siz[fx[i]];
        f[fx[i]] = fx[i];
    }
}

int main() {
    freopen("geography.in", "r", stdin);
    freopen("geography.out", "w", stdout);
    n = read(); m = read();
    for (int i = 1; i <= m; ++i) {
        int od = read(), x = read(), y = read();
        if (x > y) std::swap(x, y);
        if (od == 1) {
            int z = Find(x, y);
            r[i] = m;
            if (z) id[i] = z, h[z].id = i;
            else Add(x, y, i), id[i] = hac;
        }
        else r[h[Find(x, y)].id] = i - 1;
    }
    inv[1] = 1;
    for (int i = 1; i <= n; ++i) {
        if (i > 1) inv[i] = 1LL * (M - M / i) * inv[M%i] % M;
        f[i] = i;
        siz[i] = 1;
    }
    for (int i = 1; i <= m; ++i)
        if (r[i]) Change(1, 1, m, i, r[i]);
    Dfs(1, 1, m, 1);
    for (int i = 1; i <= m; ++i)
        printf("%d
", ans[i]);
    return 0;
}

D Medium Counting (Unaccepted)

• 神仙题不会

上午小测3

阶段排名 3

迎来了我OI生涯的首次AK，虽然满分只有200分，虽然T1都不是很懂，T2写的错解，可这都不重要啊

A 括号序列

• 这道题就是括号树的部分分，前几天看了几眼题解，还没写，然后就把之前想的和看的一丢丢题解加起来YY了一下，对拍就过了，感觉挺对，就是不知道为啥对

Show Code

#include <cstdio>
#include <cstring>

const int N = 1e6 + 5;
long long ans;
int n, f[N], stk[N], tp;
char c[N];

int main() {
    freopen("bracket.in", "r", stdin);
    freopen("bracket.out", "w", stdout);
    scanf("%s", c + 1);
    n = strlen(c + 1);
    for (int i = 1; i <= n; ++i) {
        if (c[i] == '(') stk[++tp] = i;
        else if (tp) f[i] = f[stk[tp--]-1] + 1;
        ans += f[i];
    }
    printf("%lld
", ans);
    return 0;
}

B 与 (Unaccepted)

• 考场上写了个假容斥，特判了n<=20的情况，然后就A了，考完果然就被卡了

联考day7

阶段排名 4

A 宇宙飞船

• 搞了半天没啥思路，感觉会了也不太好讲出来，就把原题解粘了过来

• 考虑如何判定一个方案是否合法。可以按编号一个个加入飞船,维护之前飞船位置的集合S,设上一个被加入的飞船位置为 x,找到 S 中比 x 大的最小元素 r 和比 x 小的最大元素 l,则新加入的飞船位置必须在 l, r 之间 (因为如果 (x, y) 跨过 l(r),就会与端点为 l(r) 的绳子相交)。

• 由此,我们可以归纳地证明出在任何一种合法方案中,考虑最后一个留在原位的飞船,前面留在原位的 x 比它小的飞船,x 一定是上升序列,x 比它大的飞船,x 一定是下降序列。并且,如果一个方案满足这个性质,那么它是合法方案。

• 所以,我们求出以每个点为结尾的最长上升子序列与最长下降子序列的和减1即可

Code

#include <cstdio>
#define Max(a, b) ({int xx = a, yy = b; xx > yy ? xx : yy;})

const int N = 2e5 + 5;

int read(int x = 0, int f = 1, char c = getchar()) {
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-') f = -1;
    for (; c >='0' && c <='9'; c = getchar())
        x = x * 10 + c - '0';
    return x * f;
}

int n, t1[N], t2[N], ans;

void Change1(int x, int w) {
    for (; x <= n; x += x & -x)
        t1[x] = Max(t1[x], w);
}

void Change2(int x, int w) {
    for (; x; x -= x & -x)
        t2[x] = Max(t2[x], w);
}

int Ask1(int x, int ans = 0) {
    for (; x; x -= x & -x)
        ans = Max(ans, t1[x]);
    return ans;
}

int Ask2(int x, int ans = 0) {
    for (; x <= n; x += x & -x)
        ans = Max(ans, t2[x]);
    return ans;
}

int main() {
    freopen("spaceship.in", "r", stdin);
    freopen("spaceship.out", "w", stdout);
    n = read();
    for (int i = 1; i <= n; ++i) {
        int x = read(), f1, f2;
        f1 = Ask1(x) + 1; Change1(x, f1);
        f2 = Ask2(x) + 1; Change2(x, f2);
        ans = Max(ans, f1 + f2 - 1);
    }
    printf("%d
", ans);
    return 0;
}

B 路径计数

• 写个hash，Dfs一遍拿了30

• 叶队随便推了个式子教给了我

Show Code

#include <cstdio>
#include <cstring>

const int N = 5e5 + 5, M = 998244353;

int read(int x = 0, int f = 1, char c = getchar()) {
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-') f = -1;
    for (; c >='0' && c <='9'; c = getchar())
        x = x * 10 + c - '0';
    return x * f;
}

int n, fac[N<<1], fai[N<<1], ans;
char c[N];

int Pow(int a, int k, int ans = 1) {
    for (; k; k >>= 1, a = 1LL * a * a % M)
        if (k & 1) ans = 1LL * ans * a % M;
    return ans;
}

int C(int n, int m) {
    if (n < 0 || m < 0 || n < m) return 0;
    return 1LL * fac[n] * fai[m] % M * fai[n-m] % M;
}

int main() {
    freopen("counting.in", "r", stdin);
    freopen("counting.out", "w", stdout);
    scanf("%s", c + 1);
    n = strlen(c + 1);
    fac[0] = 1;
    for (int i = 1; i <= n * 2; ++i)
        fac[i] = 1LL * fac[i-1] * i % M;
    fai[n<<1] = Pow(fac[n<<1], M - 2);
    for (int i = n * 2; i >= 1; --i)
        fai[i-1] = 1LL * fai[i] * i % M;
    ans = Pow(2, n) - 1;
    for (int r = 1, l = 1; r <= n; ++r) {
        if (c[r] == c[r+1]) continue;
        for (int i = l; i <= r; ++i)
            if ((ans -= (C(n, i) - C(n - r + i - 1, i) + M) % M) < 0) ans += M;
        for (int i = l; i < r; ++i)
            if ((ans += 1LL * C(n - i + l - 2, l - 2) * (i - l + 1) % M) >= M) ans -= M;
        for (int i = l + 1; i <= r; ++i)
            if ((ans += 1LL * C(n - r + i - 2, i - 1) * (r - i + 1) % M) >= M) ans -= M;
        if ((ans += 1LL * C(n - r + l - 1, l - 1) * (r - l + 1) % M) >= M) ans -= M;
        l = r + 1;
    }
    printf("%d
", ans);
    return 0;
}

C 树和森林 (Unaccepted)

• 在直径上连接拿了6分

D 编码 (Unaccepted)

• 优先队列暴力拿了30

联赛模拟测试26

阶段排名 4

A 字符交换

• 枚举每个字符，根据中位数，枚举最后聚在哪个点，贪心处理一下，总复杂度n2

• 考场上有些蒙圈，没想起来直接枚举终点，就二分了长度，枚举起点进行判断，复杂度(O(n^2log n))加了个剪枝，成为全场最优解31ms

Code

#include <cstdio>

const int N = 4e3 + 5;
int n, k, a[N], m, ans;
char c[N];

bool Judge(int len) {
    for (int i = 1; i + len - 1 <= m; ++i) {
        int l = i, r = i + len - 1, d = len - 1, s = 0;
        for (; d > 0; d -= 2, ++l, --r)
            if ((s += a[r] - a[l] - d) > k) break;
        if (s <= k) return 1;
    }
    return 0;
}

int main() {
    freopen("swap.in", "r", stdin);
    freopen("swap.out", "w", stdout);
    scanf("%d%d%s", &n, &k, c + 1);
    for (char ch = 'a'; ch <= 'z'; ++ch) {
        m = 0;
        for (int i = 1; i <= n; ++i)
            if (c[i] == ch) a[++m] = i;
        if (m <= ans || !Judge(ans + 1)) continue;
        int l = ans + 1, r = m;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (Judge(mid)) l = mid;
            else r = mid - 1;
        }
        ans = l;
    }
    printf("%d
", ans);
    return 0;
}

B 平方数

• 想到把平方项除掉，然后判断有多少相等就行，但是只会(O(nsqrt{1e9}))做法，就拿了70分

• 现在问题就是如何快速将平方数除出去

• 一个数a可以表示成(x^2y)的形式，由于a<1e9，所以x,y中只能有一个数大于1e3,所以先把1e3以内的质数除掉，最后会剩下一个数(x'^2y')

• 假设x'>1，则x'一定>1e3，以为小于的话就被筛掉了，(x'^2>1e6),因为a<1e9，所以y'< 1e3,所以y'一定为1

• 同理y'不为1的时候x'一定为1

• 这样的话筛完之后一定只剩(x'^2)或y',就判断一下是不是平方数就好了

Code

#include <cmath>
#include <cstdio>

const int N = 3e5 + 9, M = 3e5 + 7;

int read(int x = 0, int f = 1, char c = getchar()) {
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-') f = -1;
    for (; c >= '0' && c <= '9'; c = getchar())
        x = x * 10 + c - '0';
    return x * f;
}

struct Hash {
    int next, x, s;
}h[N];
int head[N], hac;

int Find(int x) {
    int ha = x % M;
    for (int i = head[ha]; i; i = h[i].next) 
        if (x == h[i].x) return h[i].s++;
    h[++hac] = (Hash) {head[ha], x, 1};
    head[ha] = hac;
    return 0;
}

int n, prime[1005], m;
long long ans;
bool v[1005];

void Primes(int n) {
    for (int i = 2; i <= n; ++i) {
        if (!v[i]) prime[++m] = i;
        for (int j = 1; j <= m && i * prime[j] <= n; ++j) {
            v[i*prime[j]] = 1;
            if (i % prime[j]) break;
        }
    }
}

bool Judge(int x) {
    int s = sqrt(x);
    return s * s == x;
}

int main() {
    freopen("square.in", "r", stdin);
    freopen("square.out", "w", stdout);
    Primes(1e3);
    n = read();
    while (n--) {
        int x = read(), y = 1;
        for (int j = 1; j <= m; ++j) {
            int cnt = 0;
            for (; x % prime[j] == 0; x /= prime[j]) cnt++;
            if (cnt & 1) y *= prime[j];
        }
        if (!Judge(x)) y *= x;
        ans += Find(y);
    }
    printf("%lld
", ans);
    return 0;
}

C 多维网络 (Unaccepted)

• 数据点分治80分，不知怎么挂了5分

D Lesson5！(Unaccepted)

• 枚举炸的点再拓扑，然而55分WA成5分了。

上午小测2

阶段排名 4

Matrix

• 手动模拟推一下式子就有了

Code

#include <cstdio>

const int N = 1e5 + 5, M = 1e9 + 7;

int read(int x = 0, int f = 1, char c = getchar()) {
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-') f = -1;
    for (; c >= '0' && c <= '9'; c = getchar())
        x = x * 10 + c - '0';
    return x * f;
}

int n, a[N], b[N], s, fac[N<<1], inv[N<<1], fai[N<<1], f1;

int C(int n, int m) {
    return 1LL * fac[n] * fai[m] % M * fai[n-m] % M;
}

int main() {
    freopen("matrix.in", "r", stdin);
    freopen("matrix.out", "w", stdout);
    n = read(); 
    fac[0] = fac[1] = inv[1] = fai[0] = fai[1] = 1;
    for (int i = 2; i < n * 2; ++i) {
        fac[i] = 1LL * fac[i-1] * i % M;
        inv[i] = 1LL * (M - M / i) * inv[M%i] % M;
        fai[i] = 1LL * fai[i-1] * inv[i] % M;
    }
    a[1] = read(); b[1] = read();
    for (int i = 2; i < n; ++i) {
        a[i] = 1LL * a[i-1] * a[1] % M;
        b[i] = 1LL * b[i-1] * b[1] % M;
    }
    f1 = read();
    for (int i = n - 2; i >= 1; --i)
        if ((s += 1LL * C(n - 2 + i, i) * read() % M * a[n-1] % M * b[i] % M) >= M) s -= M;
    if (n != 1 && (s += 1LL * read() * a[n-1] % M) >= M) s -= M;
    f1 = read();
    for (int i = n - 2; i >= 1; --i)
        if ((s += 1LL * C(n - 2 + i, i) * read() % M * b[n-1] % M * a[i] % M) >= M) s -= M;
    if (n != 1 && (s += 1LL * read() * b[n-1] % M) >= M) s -= M;
    printf("%d
", n == 1 ? f1 : s);
    return 0;
}

P & Q (Unaccepted)

• 小数据暴力，大数据瞎搞拿了27分

联赛模拟测试25

阶段排名 4

A Adore

• 暴力都没打对,原因是倒数第二层没向最后一层转移，当时都没输出一下，方案数全是0都不知道，这个样例也真是狗

• k只有10，考虑状压DP，f[i][s]表示到了第i层，状态为s的方案数，s转成二进制后，第j位是1表示到第i层第j个点的路径数为奇数，0表示为偶数

• 枚举这层的状态向下一层转移，想到只有当前点的路径数是奇数，并且与下面的点有连边，才会改变下面的点的奇偶性

• 异或运算就是用到它可以对有路径的地方快速的取反，取与是为了找到路径数既是奇数，又能和下面连边的点的个数

Code

#include <cstdio>
#include <cstring>

const int N = 1 << 11, M = 998244353;

int read(int x = 0, int f = 1, char c = getchar()) {
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-') f = -1;
    for (; c >='0' && c <='9'; c = getchar())
        x = x * 10 + c - '0';
    return x * f;
}

int n, k, f[2][N], mx, cnt[N], S, ans;

int main() {
    freopen("adore.in", "r", stdin);
    freopen("adore.out", "w", stdout);
    n = read() - 2; k = read();
    mx = 1 << k;
    for (int s = 1; s < mx; ++s)
        cnt[s] = cnt[s ^ (s & -s)] + 1;
    for (int i = 0; i < k; ++i)
        S |= read() << i;
    f[1][S] = 1;
    for (int i = 2; i <= n; ++i) {
        memset(f[i&1], 0, 4 * mx);
        int a[15] = {0}, b[15] = {0};
        for (int j = 0; j < k; ++j) {
            for (int l = 0; l < k; ++l) {
                int x = read();
                a[j] |= x << l, b[l] |= x << j;
            }
        }
        for (int s = 0; s < mx; ++s) {
            if (!f[(i-1)&1][s]) continue;
            int A = 0, B = 0;
            for (int j = 0; j < k; ++j) {
                if ((s & (1 << j)) == 0) continue;
                A ^= a[j]; B ^= b[j];
            }
            if ((f[i&1][A] += f[(i-1)&1][s]) >= M) f[i&1][A] -= M;
            if ((f[i&1][B] += f[(i-1)&1][s]) >= M) f[i&1][B] -= M;
        }
    }
    S = 0;
    for (int i = 0; i < k; ++i)
        S |= read() << i;
    for (int s = 0; s < mx; ++s)
        if ((cnt[s&S] & 1) == 0 && (ans += f[n&1][s]) >= M) ans -= M;
    printf("%d
", ans);
    return 0;
}

B Confess

• 暴力直接A了（从来没见过正解是rand的题）

• 考虑随机选两个集合交的期望

[min(sum_{i=1}^{2n}frac{C(c_i,2)}{C(n+1,2)}|sum_{i=1}^{2n}c_i=n(n+1))=frac{n-1}{2} ]

• 由于n是偶数，上式的值一定大于等于n/2，又因为有n+1个集合，所以至少有n对满足，总共有n(n+1)/2队，差不多随机n对就能得到答案

Code

#include <bits/stdc++.h>

const int N = 6e3 + 5;
std::bitset<N<<1> f[N];
int n;
char c[N/3+5];

int Get(int n) {
    return rand() % n + 1;
}

int main() {
    freopen("confess.in", "r", stdin);
    freopen("confess.out", "w", stdout);
    srand(time(0));
    scanf("%d", &n);
    for (int i = 1; i <= n + 1; ++i) {
        scanf("%s", c + 1);
        int l = strlen(c + 1), cnt = 0;
        for (int j = 1; j <= l && cnt < n * 2; ++j) {
            int x = c[j] - 33;
            for (int k = 1; k <= 6 && cnt < n * 2; ++k)
                f[i][++cnt] = (bool)(x & (1 << k - 1));
        }
    }
    while (1) {
        int x = Get(n), y = Get(n);
        while (x >= y) x = Get(n), y = Get(n);
            if ((f[x] & f[y]).count() >= n / 2)
                return printf("%d %d
", x, y), 0;
    }
    return 0;
}

C Repulsed (Unaccepted)

• (left lceil frac{n}{s} ight ceil)就有30分，加上s=1时直接输出n拿了50

D 停不下来的团长奥尔加

• 自己造一组数据模拟一下就会发现从i跳会p[i]后，从p[i]到i和之前走法是一模一样的，就直接前缀和维护一下就好了

• f[i]是第一次走到i的总距离

Code

#include <cstdio>

const int N = 1e6 + 5, M = 1e9 + 7;

int read(int x = 0, int f = 1, char c = getchar()) {
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-') f = -1;
    for (; c >= '0' && c <= '9'; c = getchar())
        x = x * 10 + c - '0';
    return x * f;
}

int n, f[N];

int main() {
    freopen("rideon.in", "r", stdin);
    freopen("rideon.out", "w", stdout);
    n = read();
    for (int i = 2; i <= n + 1; ++i)
        f[i] = (2LL * f[i-1] - f[read()] + 2 + M) % M;
    printf("%d
", f[n+1]);
    return 0;
}

上午小测1

阶段排名 3

离Ak最近的一次

木板

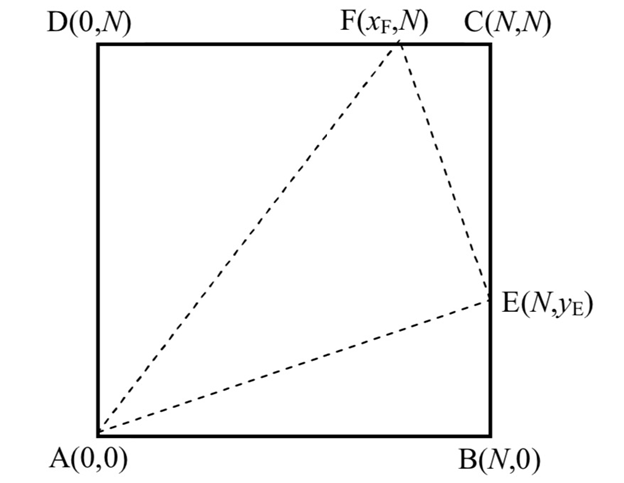
• 设BE=x,CF=y,因为三角形ABE与三角形ECF相似，得出式子

[frac{N}{N-x}=frac{x}{y} ]

• 得到y的式子

[y=frac{x(N-x)}{N}=x-frac{x^2}{N} ]

• 要满足x，y都是整数，暴力就是从1到n-1枚举x，算出y是不是整数

• 发现只有在(x^2)整除N的时候y是整数，这样的话(x^2)一定包含N的所有质因数，把N进行质因数分解，x的最小取值也就有了

[N=p_1^{c_1}p_2^{c_2}...p_m^{c_m} ]

[x_{min}=p_1^{left lceil frac{c_1}{2} ight ceil}p_2^{left lceil frac{c_2}{2} ight ceil}...p_m^{left lceil frac{c_m}{2} ight ceil} ]

• 只需要在1～N-1中找到可以整除(x_{min})的数的个数再乘8就是答案

• 乘8是因为有4个角，每个角连出的中间的三角形的直角顶点有两种情况

Code

#include <cstdio>
#define int long long 

int n;

signed main() {
    freopen("tri.in", "r", stdin);
    freopen("tri.out", "w", stdout);
    while (1) {
        scanf("%lld", &n);
        if (!n) break;
        int x = n, s = 1;
        for (int i = 2; i * i <= x; ++i) {
            if (x % i) continue;
            int cnt = 0;
            for (; x % i == 0; x /= i) cnt++;
            cnt = cnt + 1 >> 1;
            while (cnt--) s *= i;
        }
        if (x > 1) s *= x;
        printf("%lldn", (n - 1) / s * 8);
    }
    return 0;
}

序列

• 倍增加二分瞎搞，还没判公比的范围就拿了95，差一点就AK了，后来还发现公比还算错了，用的gcd，随便造一组数据就能卡掉

• 一个数是若干个数的的若干次幂，定义这个数的最小底数是这若干个数的最小值，求法就是将这个数质因数分解，每个质因数的指数都除以所有指数的最大公约数算出来的数

[x=p_1^{c_1}p_2^{c_2}...p_m^{c_m} ]

[g=gcd(c_1, c_2, ..., c_m) ]

[f(x)=p_1^{frac{c_1}{g}}p_2^{frac{c_2}{g}}...p_m^{frac{c_m}{g}} ]

• 一段连续的区间符合条件必须满足没有相同的数（公比为1的情况另扫一遍即可），而且每相邻两个数的商的最小底数都相同，这样就是等比序列了

• 这道题要求公比不能超过1000，可以直接把以1000以内的数的所有不超过1e18的幂都放进map里，实测共有6624个数，然后查最小底数就在map里查询

• 预处理出b[i]表示a[i-1]与a[i]的商的最小底数，双指针扫一遍即可求出答案

Code

#include <set>
#include <map>
#include <cstdio>
#define int long long

const int N = 1e5 + 5, M = 1e18;

int read(int x = 0, int f = 1, char c = getchar()) {
    for (; c < '0' || c > '9'; c = getchar())
        if (c == '-') f = -1;
    for (; c >='0' && c <='9'; c = getchar())
        x = x * 10 + c - '0';
    return x * f;
}

std::map<int, int> m;
std::multiset<int> st;
int n, a[N], b[N], ans;

int Cal(int x, int y) {
    if (x > y) std::swap(x, y);
    if (!x) return -1;
    int d = y / x;
    return d * x == y ? d : -1;
}

signed main() {
    freopen("seq.in", "r", stdin);
    freopen("seq.out", "w", stdout);
    for (int i = 2; i <= 1e3; ++i) {
        if (m[i]) continue;
        for (int x = i; x <= 1e18 && x > 0; x *= i)
            m[x] = i;
    }
    m[1] = m[-1] = 0;
    n = read();
    for (int i = 1, s = 0; i <= n; ++i) {
        a[i] = read();
        b[i] = m[Cal(a[i-1], a[i])];
        s = a[i] == a[i-1] ? s + 1: 1;
        if (s > ans) ans = s;
    }
    for (int i = 1, l = 1, q = 0; i <= n; ++i) {
        if (!q) q = b[i];
        else if (q != b[i]) q = 0;
        if (!b[i] || !q) st.clear(), l = i, q = 0;
        while (st.find(a[i]) != st.end()) st.erase(a[l++]);
        if (i - l + 1 > ans) ans = i - l + 1;
        st.insert(a[i]);
    }
    printf("%lld
", ans);
    return 0;
}