CF 166E Tetrahedron

E. Tetrahedron

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given a tetrahedron. Let's mark its vertices with letters A, B, C and D correspondingly.

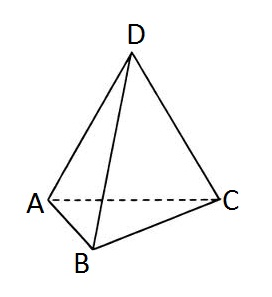
An ant is standing in the vertex D of the tetrahedron. The ant is quite active and he wouldn't stay idle. At each moment of time he makes a step from one vertex to another one along some edge of the tetrahedron. The ant just can't stand on one place.

You do not have to do much to solve the problem: your task is to count the number of ways in which the ant can go from the initial vertex D to itself in exactly n steps. In other words, you are asked to find out the number of different cyclic paths with the length of n from vertex D to itself. As the number can be quite large, you should print it modulo 1000000007 (10⁹ + 7).

Input

The first line contains the only integer n (1 ≤ n ≤ 10⁷) — the required length of the cyclic path.

Output

Print the only integer — the required number of ways modulo 1000000007 (10⁹ + 7).

Examples

input

Copy

2

output

Copy

3

input

Copy

4

output

Copy

21

Note

The required paths in the first sample are:

• D - A - D
• D - B - D
• D - C - D

 

【题意】

给一个四面体，从顶点D沿棱走n步回到D,问方案数。

 

【分析】

 

笔者高中的时候记得在数学试卷上做过类似的题目， 不过当时是求概率的，所以笔者一看到这道题目的时候就是往概率上想，而走n步的情况总可能就是3的n次方，所以只要求出走n步到达D点的概率，用它乘以总可能的情况数并对10的9次方加7取余便是最终的答案，这里设P(A, n)为第n次到A点的概率，所以P(A, n) + P(B, n) + P(C, n) + P(D, n) = 1; 且由于对称性可以知道，P(A, n)  = P(B, n) = P(C, n), 即P(A, n) = 1/3 * (1 - P(D, n))(1),而第n次到达D点，说明第n - 1次在A, B, C 中的其中一点，而又由于对称性可得，P(D, n) = 1/3*(P(A, n - 1) + P(B, n - 1) + P(C, n - 1)) = P(A, n - 1); 与(1)式联立得P(D, n + 1) = 1/3 * (1 - P(D, n)); 利用高中数列知识可以求得;则第n次到达D点的方法数等于总数(3 ^ n)乘以概率，设第n次到达D点的方法数为dp[n], 则有

;这个可以直接用暴力写，也可以用矩阵快速幂写，在这就不贴代码了，不过高中学过数学竞赛的同学可能会觉得这个式子结构()有点眼熟, 3和-1的次数都是等次幂，让人联想到线性递推数列的求解 : 对于数列An = p * An-1 +  q *An-2, 其特征方程为x^2 = px + q, 假设其两根分别为x1, x2,则(x1, x2不相等时)或(x1 = x2时)，a,b为常数，可由给出条件获得，所以可以把中的3和-1分别看成x1,x2,由二次方程(设为x^2 + px + q = 0)的韦达定理的p = -(x1 + x2) = -2, q = x1 *x2 = 3;即方程为x^2 - 2x - 3 = 0,而此方程为数列An = 2 * An-1 +  3 *An-2

的特征方程，由此我们可以得到一个递推关系式为dp[n] = 2 * dp[n - 1] + 3 *dp[n - 2];

 引自__http://www.cnblogs.com/zyf0163/p/4318036.html

 

【代码】

#include<cstdio>
using namespace std;
const int N=1e7+5;
const long long mod=1e9+7;
int n;long long f[N];
int main(){
	f[1]=0;f[2]=3;
	scanf("%d",&n); 
	for(int i=3;i<=n;i++){
		f[i]=2*f[i-1]+3*f[i-2];
		f[i]%=mod;
	}
	printf("%I64d
",f[n]);
	return 0;
}