[NOI2013]书法家

题目描述

小E同学非常喜欢书法，他听说NOI2013已经开始了，想题一幅“NOI”的字送给大家。

小E有一张非常神奇的纸，纸可以用一个n 行m 列的二维方格矩阵来表示，为了描述方便，我们定义矩阵左下角方格坐标为(1,1) ，右上角方格坐标为(m,n) 。矩阵的每个方格有一个整数的幸运值。在格子上面写字可以增加大家的幸运度，幸运度的大小恰好是所有被笔写到的方格的幸运值之和。现在你要在上面写上 ‘N’，‘O’，‘I’三个字母。

下面给出3个书法字的定义：

1.‘N’由若干（≥3）个边平行于坐标轴的矩形组成，设有K个矩形组成（标号1~K），第i个矩形的左下角方格坐标设为(Li ,Bi) ，右上角坐标设为(Ri ,Ti) ，要求满足：

a)Li<=Ri,Bi<=Ti

b)对任意1<i<=K，有Li=R(i-1)+1

c)对任意3<=i<K，有B(i-1)<=Ti<=T(i-1),Bi<=B(i-1);

d)B2>B1,T2=T1,B(K-1)=B(K),T(k-1)<T(K)

2.‘O’由一个大矩形A，挖去一个小矩形B得到，这两个矩形的边都平行于坐标轴。设大矩形左下角的方格坐标为(u,v)，长为W宽为H，则小矩形B满足左下角方格坐标为(u+1,v+1) ，长W-2 ，宽H-2。要求满足：

a)W>=3,H>=3

b)u>R(K)+1

3.‘I’为3个边平行于坐标轴的从下到上的实心矩形组成，从下到上依次标号为1,2,3，第i 个矩形的左下角格子坐标设为(Pi , Qi )，右上角格子坐标设为(Gi , Hi )，要求满足：

a)Pi<=Gi,Qi<=Hi
b)P1=P3>u+W,G1=G3
c)Q1=H1=Q2-1,H2+1=Q3=H3
d)P1<P2<=G2<G1

下图是一个‘N’,‘O’,‘I’的例子

另外，所有画的图形均不允许超过纸张的边界。现在小E想要知道,他能画出的最大幸运度是多少。

输入输出格式

输入格式：

输入文件penman.in的第一行包含两个正整数n和m，分别表示矩阵的行数和列数。

接下来n行，每行有m个整数，第i+1行的第j个数表示格子(j,n-i+1)的幸运值。

输出格式：

输出到文件penman.out中，输出一个整数T，表示小E能够获得的最大幸运度。

输入输出样例

输入样例#1：

【样例输入1】
3 13 
1 1 -1 -1 1 -1 1 1 1 -1 1 1 1 
1 -1 1 -1 1 -1 1 -1 1 -1 -1 1 -1 
1 -1 -1 1 1 -1 1 1 1 -1 1 1 1 




【样例输入2】
3 13
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1

输出样例#1：

【样例输出1】
24 
【样例输出2】
-20

说明

样例1

样例2

数据范围

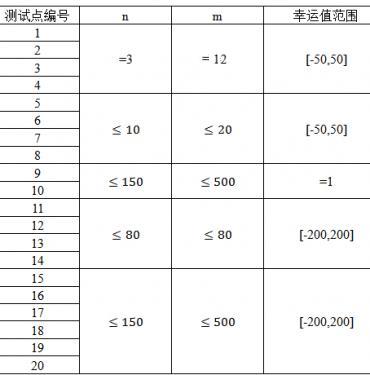
对于所有的测试数据，保证n≥3，m≥12。

据说状态是这样的：

so，贴了份代码。表示没有耐心把它打完。

#include<cstdio>
#include<iostream>
using namespace std;
const int oo=-150000000;
int f[3][9][151][151],cnt,m1,p1,t,mx[151][151],n,m,ans=oo,max5=oo,max2=oo,a[501][151],s[501][151];
int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%d",&a[j][i]);
            s[j][i]=s[j][i-1]+a[j][i];
        }
    }
    for(int i=0;i<9;i++){
        for(int j=0;j<151;j++){
            for(int k=0;k<151;k++){
                f[0][i][j][k]=oo;
            }
        }
    }        
    for(int j=0;j<151;j++){
        for(int k=0;k<151;k++){
            mx[j][k]=oo;
        }
    }        
    cnt=0;m1=2;p1=1;
    for(int i=1;i<=m;i++){
        t=m1;m1=cnt;cnt=p1;p1=t;
        for(int j=1;j<=n;j++){
            for(int k=j+1;k<=n;k++){
                f[cnt][0][j][k]=max(f[m1][0][j][k],0)+s[i][k]-s[i][j-1];
            }
        }
        for(int j=1;j<=n;j++){
            mx[1][j]=f[m1][1][1][j];
            for(int k=2;k<=j;k++){
                mx[k][j]=max(mx[k-1][j],f[m1][1][k][j]);
            }
        }
        for(int j=1;j<=n;j++){
            f[cnt][1][j][j]=max(mx[j][j],mx[j-1][j-1])+a[i][j];
            for(int k=j+1;k<=n;k++){
                f[cnt][1][j][k]=max(f[cnt][1][j][k-1]+s[i][k]-s[i][k-1],mx[j][k]+s[i][k]-s[i][j-1]);
            }
        }
        for(int j=1;j<n;j++){
            int max0=oo;
            for(int k=n-1;k>=j;k--){
                max0=max(max0,f[m1][0][j][k+1]);
                f[cnt][1][j][k]=max(f[cnt][1][j][k],max0+s[i][k]-s[i][j-1]);
            }
        }
        for(int k=2;k<=n;k++){
            int max1=oo;
            for(int j=k-1;j;j--){
                max1=max(max1,f[m1][1][j+1][k]);
                f[cnt][2][j][k]=max(f[m1][2][j][k],max1)+s[i][k]-s[i][j-1];
            }
        }
        if(i>1){
            for(int k=2;k<=n;k++){
                for(int j=k-1;j;j--){
                    max2=max(max2,f[p1][2][j][k]);
                }
            }
        }        
        for(int j=1;j<n-1;j++){
            for(int k=j+2;k<=n;k++){
                f[cnt][3][j][k]=max2+s[i][k]-s[i][j-1];
                f[cnt][4][j][k]=max(f[m1][3][j][k],f[m1][4][j][k])+a[i][k]+a[i][j];
                f[cnt][5][j][k]=f[m1][4][j][k]+s[i][k]-s[i][j-1];
            }
        }
        if(i>1){
            for(int j=1;j<n-1;j++){
                for(int k=j+2;k<=n;k++){
                    max5=max(max5,f[p1][5][j][k]);
                }
            }
        }        
        for(int j=1;j<n-1;j++){
            for(int k=j+2;k<=n;k++){
                f[cnt][6][j][k]=max(max5,f[m1][6][j][k])+a[i][k]+a[i][j];
                f[cnt][7][j][k]=max(f[m1][6][j][k],f[m1][7][j][k])+s[i][k]-s[i][j-1];
                f[cnt][8][j][k]=max(f[m1][7][j][k],f[m1][8][j][k])+a[i][k]+a[i][j];
                ans=max(ans,f[cnt][8][j][k]);
            }
        }
    }
    printf("%d
",ans);
    return 0;
}